Pitching a ballcurve

by Burkard Polster and Marty Ross

The Age, 24 June 2013

It's that time again. Wimbledon begins today, promising us two weeks of excellent, nail-biting tennis. And then in the finals Djokovic will beat Nadal, and Serena will thrash whomever.

So, that's about it for the tournament. On with the maths.

We've already written plenty on tennis: the tournament numbers; the seeding; the scoring; and Hawk-Eye. Now it's time to take a look at the balls.

What's there to say about a tennis ball? It's, um, ball-shaped and perhaps that's about it. But perhaps not.

Who would have guessed, for example, that Wimbledon's old tennis balls become homes for the Eurasian harvest mouse? (Warning: ridiculously cute picture at the previous link.) Unfortunately, that charming story is not very mathematical, so we should probably leave it for the Mouse Masters to tell.

Instead, we'll take a look at the strange curve formed by the seam on a tennis ball. The first and very natural question is, why is it there? The answer is, it just is.

The tennis ball seam is an artefact of the manufacturing process, of gluing the two pieces of felt onto the rubber ball underneath. Moreover, unlike the seams of baseballs and cricket balls, the seam on a tennis ball has no significant effect on the throw or the flight of the ball.

Nonetheless, even if immaterial for the game, the seam still forms an interesting, and nicely mathematical, curve. The simplest way to construct a tennis ball curve is to draw four identical touching circles, as shown on the left, below.

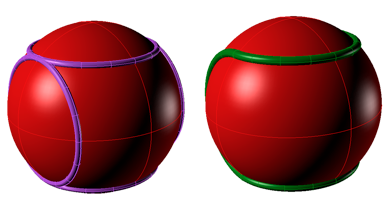
Taking half of each circle, the four semicircles combine to form the tennis ball curve.

It is easy to see that the tennis ball curve cuts the ball's surface into two identical pieces. (That is, the covering of a tennis ball is formed from two identical pieces of felt.) What is a little less obvious is that the curve itself is symmetric in an elegant yin-yang fashion.

Take a point on the curve where two of the semicircles meet. The antipodal point (the point on the exact opposite side of the ball) will also be such a meeting point. Then, rotating 180 degrees around the diameter through these points swaps the two pieces of the surface, keeping the curve as a whole in place.

This bisection of the tennis ball's surface can also be performed on a solid ball. Just imagine taking a knife and cutting all along the curve into the centre of the ball. The result will be two identical solid pieces, fitting together as an impressive 3D yin-yang:

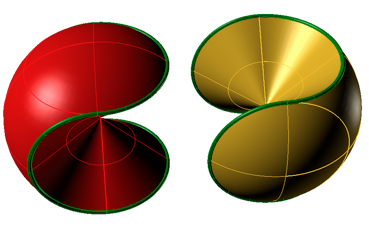
If this is all very pretty it is not overly deep. However, the tennis ball curve also illustrates some genuinely deep mathematics, a surprising and beautiful result known as the tennis ball theorem.

Consider again the meeting points of the semicircles. They are inflection points, meaning they are points where the path changes from curving in one direction (say, to the left) to curving in the opposite direction (to the right). The tennis ball curve has four inflection points in total, being the four meeting points.

Now, imagine any curve that dissects the tennis ball surface into two pieces of equal area. The dividing curve and the two pieces needn't be symmetric in any manner. How many inflection points must the curve have?

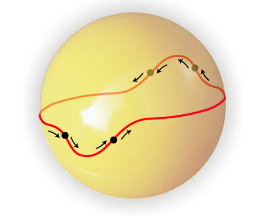
The answer is, there needn't be any inflection points at all. If we simply cut the ball along its equator then the two hemispheres on either side will of course have equal area, and the equatorial curve has no inflection points. But it turns out this case is very special.

The tennis ball theorem states that, excepting the special equatorial case, any curve that cuts the surface of the ball into two pieces of equal area must have at least four inflection points. That is, the tennis ball curve is in a certain sense the very simplest we can arrange.

A straightened version of the tennis ball curve also solves a more familiar puzzle. Let’s morph our tennis ball into a cube, and then the curve can follow along the edges:

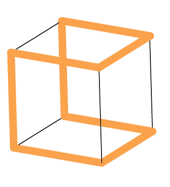
The curve still symmetrically divides the surface into two pieces, and it now has an added property: the curve gives us a Hamiltonian circuit, meaning every corner of the cube is visited exactly once.

Hamiltonian circuits are interesting creatures in themselves, but the tennis ball circuit has a particularly special property. The Hamiltonian circuit of the cube encodes a systematic method of solving the famous towers of Hanoi puzzle when our tower consists of three rings.

And what if our tower of Hanoi consists of four rings? That can be solved, too, and all we need is a 4-dimensional tennis ball. However, we’ll probably have to make those ourselves: Nadal and Djokovic would probably refuse to play with them, and the Eurasian harvest mice would definitely not be amused.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators (and iPads) with a hammer.