Seeds of doubt

It’s tennis time. The French Open is in full swing and we’re all anticipating a terrific Djokovic-Nadal final. True, Roger Federer may upset that plan. If he does, Novak Djokovic may have good cause to complain.

A Grand Slam tennis draw consists of 128 players arranged in a knockout tournament. Of course the draw is not totally random. The top 32 players are seeded and the draw is arranged so that these seeded players can only meet in the later rounds.

It is questionable why Djokovic is the top seed at the French Open, given that Rafael Nadal has the clear edge on the clay courts of Roland Garros. However, seeding players is complicated and imprecise, making it difficult to avoid such quirks. Still, there are some very strange things afoot.

Being the top two seeds, Djokovic and Nadal are placed in separate halves of the draw. Similarly, the top four seeds are in their own quarters, the top eight seeds are handled in the same manner, and so on. Finally, with the 32 seeds in place, the remaining 96 spots are randomly allotted to the cannon fodder. (With all due apologies to Gustavo Kuerten.)

Actually, it appears that the assigning of those final spots is not always as random as is claimed, which makes for an interesting story. However, we’ll focus upon the top players.

Barring upsets, the seeded players will eventually meet, but what then? Supposing, for example, that the top four players make it through to the semifinals, who is to play whom? That’s when things get weird.

There are three ways that the top four seeds might be scheduled to meet, of which the most natural would appear to be 1 v 4 and 2 v 3. A second possibility, 1 v 2 and 3 v 4, is wisely precluded by the rules.

What about the third possibility, with 1 v 3 and 2 v 4? It’s difficult to see any argument for this arrangement, which typically advantages the second seed over the first. Nonetheless, the Victorian Football League once used this system for its finals. Grand Slam tennis tournaments have a system almost as peculiar.

According to the Grand Slam rules, the 3rd and 4th seeds are placed in distinct quarters of the draw and away from the two top seeds, but otherwise are placed randomly. (There is then a similar random process used to place the lower seeds.) This means that there is a 50-50 chance that the draw will point towards semifinals of 1 v 3 and 2 v 4.

Such dice-rolling seem remarkably amateurish for a multi-zillion dollar sport. And, as the dice would have it, in the current French Open the top seed Djokovic is scheduled to meet 3rd seeded Federer, while Nadal can look ahead to the significantly easier (if not easy) 4th seeded Andy Murray. Perhaps that is justice, since arguably Rafa “should” be top seed. Nonetheless, Novak appears to have good reason to feel aggrieved.

But maybe the Grand Slam bosses know more than it seems. In what sense can we be sure that 1 v 4 and 2 v 3 is the best pairing? The question is surprisingly tricky.

Let’s assume that the seeding is accurate, that Djokovic is stronger than Nadal, who is stronger than Federer, who is stronger than Murray. We’ll also assume that every player has less chance of beating a higher seed than a lower seed; for example, Murray has less chance of beating Djokovic than he has of beating Nadal.

With these assumptions, 1 v 4 and 2 v 3 can be shown to be a natural pairing in many respects. In particular, Djokovic has a greater overall chance of winning than Nadal, who has the next greatest chance, and so on. Moreover, 1 v 4 and 2 v 3 is the only pairing that is always fair in this sense.

However, the natural pairing does not necessarily give the greatest chance of a Djokovic-Nadal final. Suppose that the winning chances between the four players are as follows:

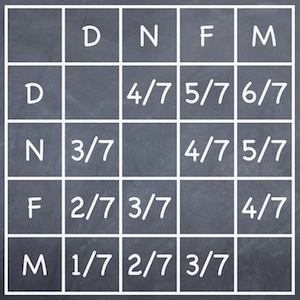
The table indicates, for example, that Nadal has a 4/7 chance of beating Federer, and conversely Federer has a 3/7 chance of beating Nadal.

In this scenario, the pairing 1 v 4 and 2 v 3 gives a 24/49 chance of a Djokovic-Nadal final. However, the pairing 1 v 3 and 2 v 4 does slightly better, giving a 25/49 chance of the dream final.

Analysing the top eight seeds requires considerably more work: there are 315 possible arrangements of the eight seeds in the quarter finals, of which 48 are consistent with the Grand Slam rules. And, many strange things can happen.

The most natural pairing is usually considered to be 1 v 8, 4 v 5, 2 v 7 and 3 v 6, but it is difficult to say why. Many things can go wrong, and in particular this pairing is not always fair in the sense described above.

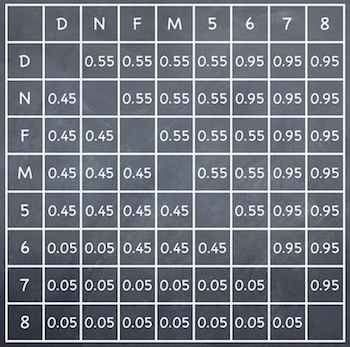
Imagine the winning chances of the top eight seeds against each other are as in the table above. Then the “natural pairing” will actually give second seed Nadal about a 35% chance of winning the final, with top seed Djokovic only a 30% chance.

So, maybe the Grand Slam chiefs are cleverer than we thought. Perhaps all that randomness in the draws is a brilliant way to cope with some tricky mathematics. Perhaps … Nah! It’s still a silly idea and Djokovic still has every right to be grumpy.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.