Sigh! It's time for Pi

What, so after last week’s pummeling of the golden ratio, now your Maths Masters are picking on π? Are there no numbers of which we actually approve?

Don’t worry; of course we’re big fans of π. (We’re also fans of the golden ratio, once stripped of the beauty nonsense.) However, Pi Day is approaching, and we always greet this day with mixed emotions.

This coming Thursday is March 14, or 3/14 as those weird Americans write it. That looks like 3.14, which is π-ish, and voilà: Pi Day!

Pi Day has been celebrated since 1988, when physicist Larry Shaw of San Francisco’s superb Exploratorium Museum came up with the idea. It’s a great gimmick, a way of grabbing the attention of news outlets seldom keen to report on mathematics. We’ve eagerly celebrated Pi Day on a number of occasions.

The problem is that there is one aspect of the reporting on π that is seriously misguided: the worship of its decimal expansion. Regular readers of this column will be well aware of our distaste for decimals, and the obsession over the digits of π is an archetypal example of all that is wrong with a focus on decimals.

Just about any significant rise in computing power is quickly followed by the thoroughly predictable news report that some clever fellow has been able to compute another zillion digits of π. The current record, set in 2011, stands at 10 trillion (10,000,000,000,000) digits. But why should anyone care?

We're reluctant to object to quirky news stories about mathematics. However, whatever the computing prowess required, there is much less mathematics here than meets the eye, and no deep mathematical purpose. The danger is that readers of these news stories will confuse digit-chasing with important and genuinely interesting mathematical research. The very gimmick of Pi Day being on 3/14 actively encourages this confusion.

Why decimals? Why not a binary expansion of π, or ternary? Any base is just as (not very) meaningful. Yes, most of us have ten fingers, but this biological happenstance has no bearing on the intrinsic nature of π.

Of course knowing something of the value of π is definitely worthwhile. π is first and foremost a circle thing, the ratio of the circumference of a circle and its diameter, and circles are more than a little important to science and technology. As such, estimating π has a long and proud history (engagingly told in the eccentric and funny book by Petr Beckmann).

Perhaps the simplest method of estimating π is to wrap a rope around a wheel, unwind the rope and measure its length. However that’s not very mathematical and is unlikely to be too accurate. (Maybe it is experiments such as this that led to the Old Testament implying π is equal to 3.)

The simplest mathematical approach to estimating π is to approximate a circle by polygons:

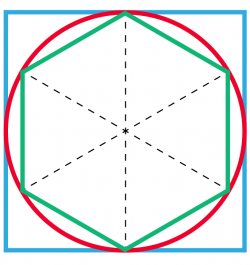
Placing a square outside a circle of diameter 1 and a regular hexagon inside, it follows that π must lie between 3 and 4. No more precise than we could achieve with wheel and rope, but an elegant beginning.

Around 2000 BC the Babylonians used the value 3 1/8 for π, and around the same time the Egyptians used the remarkable value of (16/9)², about 3.16. The Egyptians' estimate was obtained by approximating a circle by a regular octagon.

Of course it was the great Archimedes of Syracuse who mastered the art of polygonal approximation, around 250 BC. Using 96-sided polygons (and an ingenious computing procedure), Archimedes was able to show that π must lie between 3 10/71 and the familiar 3 1/7 (= 22/7): for decimal fans, that implies π is between 3.140 and 3.143, plenty good enough for the engineering of Archimedes' time, and for the majority of today’s engineering.

Around 250 AD, the great Chinese mathematician Liu Hui discovered a technique similar to Archimedes'. Liu’s methods were continued by Zu Chongzhi; around 500 AD, Zu demonstrated that π was trapped between 3.1415926 and 3.1415927, and also presented the beautiful and remarkably accurate fractional approximation 355/113.

The accuracy of these approximations is all the more impressive given the cumbersome nature of the geometric techniques employed. And, when the new-fangled calculus was introduced in the 17th century, the digit-masters really went to town. By the 18th century, more than 100 digits of the decimal expansion of π were known, about 80 more digits than any practical application could ever conceivably require.

Now we have electric computers, refined techniques, and zillions of digits of π. Can we do anything with them?

The most natural question is whether the digits of π begin to repeat, which amounts to asking whether π is a fraction. In some psychological (and very non-mathematical) sense, if the digits we know of were to repeat that would suggest π is a rational number; conversely, the fact that no repetition appears in the zillion known digits suggests that π is irrational.

Probably a few hundred digits suffices for this fundamentally pointless game. And, even those zillions of digits cannot prove anything about the rationality or irrationality of π.

That π is indeed irrational was established in 1766 by the Swiss mathematician Johann Heinrich Lambert. His proof used absolutely nothing about the digits of π. (A beautiful calculus-based proof of the irrationality of π, due to mathematician Ivan Niven, can be found here (p. 76)).

So all those digits of π are pretty useless. But perhaps there is still something interesting we can ask about them. Perhaps.

Here’s a sample question: how many 9s are there in the expansion of π? It would seem obvious that there ought to be infinitely many 9s, but in fact no one has any idea. The same is true of almost any question about the digits one might think to ask.

Yes, amongst those zillions of known digits, the 9s seem to appear around 10% of the time, in a random manner. But those zillion digits give no real clue as to what is true about the infinitely many digits that follow, or how one might prove anything about them.

However, there is probably one worthwhile insight gained from calculating all those digits. It suggests that, contrary to popular suspicion, mathematicians are very much human beings. And, what mathematicians choose to investigate can be as irrational as the irrational number that inspires them.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.