The golden ratio must die!

by Burkard Polster and Marty Ross

The Age, 4 March 2013

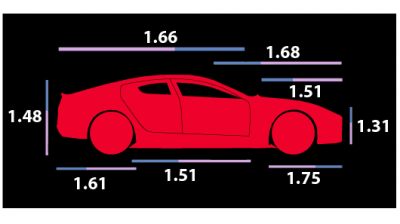
As a child, one of your Maths Masters was fascinated by cars. His favourite was an Aston Martin; the DB5 was a very cool sports car with the added attraction that James Bond drove one. Now, with this week’s release of the Rapide S, these iconic cars are iconic in a special new way: according to The New York Times, the latest Aston Martin is designed boot to bonnet in terms of the golden ratio.

Sigh! So here we are again.

The golden ratio, about 1.62, is usually denoted by the Greek letter φ (phi). It is one of the most famous, and infamous, of numbers. The golden ratio lies at the heart of some beautiful mathematics. Unfortunately, as we have discussed previously, φ is also promoted as the number beyond numbers, the key to life, the universe and everything. It has been the unceasing inspiration for cultish nonsense.

Prior to Aston Martin, it was Venus & Olay applying golden ratio magic to determine stylish dress lengths. (We’re fans of Lily Serna, but she and The Australian really should have known better.) And before that, φ was heralded as the key to determining the most fertile uteruses. (Alex Bellos and The Guardian should have known better as well.)

It never seems to end. But now, with the desecration of James Bond’s car, we’ve finally had enough. Once and for all, we’re determined to destroy the golden ratio cult.

To begin, let's be clear that φ is not simply this magic number that has fallen from the sky, and it is not exactly 1.62. In contrast to the vast majority of media reports, we'll precisely determine our target.

Though the name “golden ratio" appears to have originated in the 19th century the concept dates back at least to the Greek mathematician Euclid. To facilitate certain geometric constructions, Euclid sought to divide a line segment into a big part and a small part in a special way, as illustrated below.

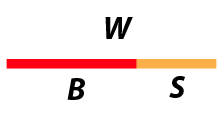
Writing W for the length of the whole line, and B and S respectively for the big and small parts, Euclid wanted the lengths to be related by the equation

W/B = B/S

This common ratio is what we now refer to as φ, the golden ratio. A little algebra shows that φ is the solution to a quadratic equation, from which it follows that φ = (1 + √5)/2, about 1.618, but actually an irrational number.

Related to φ, and with similarly humble Greek origins, is the concept of a golden rectangle. A rectangle is said to be golden if it is of just the right shape so that removing a square leaves a (rotated) rectangle of the same shape.

It is not too difficult to show that a rectangle is golden exactly if its length divided by its width is equal to φ.

All that is fine and it leads to some beautiful mathematics. And, the simple ideas underlying φ mean that it can elegantly model some naturally occurring phenomena. (Even if other purported appearances of φ in nature, such as in the nautilus shell, are utter bollocks.)

But let’s talk aesthetics. Is the golden ratio, as is so often claimed, the key to beauty?

The answer is emphatically no. Moreover, not only is the golden ratio not the key to beauty, it cannot be. As we shall explain, the notion is fundamentally absurd.

Of course there are constant claims that great artists and architects have used the golden ratio or golden rectangles in their works. However, almost always these claims are supported by no evidence beyond the exhibition of some ratio that is roughly equal to φ. And it is not unusual for the ratio to be very rough: people hardly ever check.

Consider, for example, the new Aston Martin. The stylish website pictures the Rapide S with supposedly golden ratios marked every which way. However, as our graphic above illustrates, the segments determining these ratios appear to be quite arbitrary, and many of the resulting ratios are nowhere near φ. It may still be true that the Rapide S was designed with the golden ratio in mind, but it is telling that the company's own graphics suggest the opposite.

Now, even supposing some great artist used φ in their work, what is the evidence that φ is the key to the greatness of their art? What is the evidence that φ itself is beautiful? There is none. Not a scrap.

There have probably been hundreds of experiments on people's preferences for certain ratios. Barely a year goes by without some poor university Psych class being interrogated over a bunch of rectangles. The main conclusion that can be drawn is that people's stated preferences depend very subtlely on how they are asked.

Consider the three rectangles pictured below.

Most people will choose the middle rectangle as the most pleasing. For some that's simply because it is the middle in position; or, it may be because it's the middle in proportion. Or it may well be that there is a general dislike of rectangles that are too squarish or too skinny. However, even if true, it is an astronomical leap to go from people's vague preference for not-square-and-not-skinny rectangles to precise conclusions about golden rectangles. (In fact, the middle rectangle rectangle above has length-to-width ratio of 1.7: it's our first step in starting a new cult.)

Most experiments that even remotely support φ being the key to beauty involve some (probably unconcious) push polling of the type above. And many experiments offer no such evidence at all. Below are a selection of rectangles from the superb debunking article by mathematician George Markowsky. Have fun choosing your favourite, and have fun finding the golden rectangle.

At this stage it should be clear why any attempt to prove that φ is the key to beauty is doomed to failure. An experiment may indicate a commonly held and rough preference for certain ratios, and that could be interesting. But an experiment simply cannot hone in on a precise number.

The limitation of human senses ensure that no experiment can distinguish a preference for φ over 1.618 or 1.62, or probably even 1.6. There is not a shred of evidence that the golden ratio is any more beautiful than boring old 8/5, and we very much doubt there ever will be.

So, we've done it: the golden ratio is dead and we can all relax. Hardly.

People have been debunking golden ratio nonsense for as long as the nonsense has been around. In 1922, art critic Theodore A. Cook wrote a brilliantly scathing article entitled A New Disease in Architecture. It said all that was needed about the burgeoning golden ratio cult and the whole absurd notion of reducing beauty to a number: "There is no short cut to the beautiful, no formula for the creation of the perfect."

Cook's article did no good. Markowsky's article referred to above did no good. Golden ratio silliness has been debunked over and over and over and over again, and it never does any good. We predict that the next Bond movie will feature James driving his special Aston Martin φ-car, and with the beautifully φ-proportioned Bond girl in her special φ-dress, and ... well, we don't dare ponder further.

We'll continue to fight. We'll hammer the φ cult whenever it appears. But we are fully aware that it will never do any good. The golden ratio is a zombie number: no matter how many times it is killed, it will always rise again.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.