Infinitely and definitely, Terry Tao is prime

By Burkard Polster and Marty Ross

The Age, 28 July 2008

Prime numbers are maddening. Individually, they are as simple as possible. But, collectively, they are the most puzzling creatures in mathematics. Even for the brilliant Australian mathematician Terry Tao.

The importance of primes is their role as numerical building blocks. For example, 60 equals the prime product 2 x 2 x 3 x 5. And, as Euclid proved, any whole number can similarly be factored into primes.

That is easy, but when we try to locate primes, things get weird. Yes, all primes excepting 2 are odd, but can we say anything else? The table highlights the primes below 180. Is there a pattern?

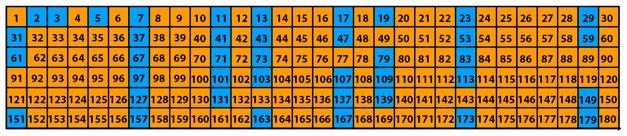
The full column 7, 37, ... , 157 stands out. This is an arithmetic sequence of primes, where we’re adding 30 each time. But, we’ve stopped our table just in time: adding 30 to 157 gives 187, and 187 = 11 x 17 is not prime.

The table suggests that the higher we look the rarer primes become. Do they stop completely? If we have no pattern, how do we know there will always be a next prime, that there are infinitely many primes?

Once again, Euclid provided the answer. To make the question concrete, suppose we have stumbled upon the primes 2, 7, 13 and 23. How can we use these primes to guarantee there is another one?

Euclid’s beautiful argument goes as follows. Collect the primes we already have, and form the number N = (2 x 7 x 13 x 23) + 1. If N is prime we are done, but that may not be the case. However, it is easy to see that N is not divisible by any of the primes we started with: dividing N by 2, 7, 13 or 23 leaves a remainder of 1. But, N definitely has prime factors, and so all those primes must be new. Quite Easily Done.

Notice that the number N will be big, and Euclid’s process gives no easy method to actually identify the new primes. For example, in our case with N = 4187, what are the new primes? We’ll leave that for you to puzzle over.

But didn’t Euclid settle all these prime questions thousands of years ago? To demonstrate how troublesome primes still are, let us consider twin-primes. A twin-prime is a pair, such as 3-5 or 11-13, with a gap of 2 between.

It is easy to find examples of twin-primes. But, as primes become scarce, twin-primes become very scarce. Are there infinitely many twin-primes? No one knows!

Here is another problem. Suppose we look for arithmetic sequences of primes. Our table contains a sequence of six primes. Can you find an arithmetic sequence of seven primes? That’s another (very difficult) puzzle for you.

Are there arithmetic sequences of primes of any length we like? Yes, but this was only proved in 2004, by Terry Tao together with the mathematician Ben Green. This led to Terry receiving the Fields Medal, the highest honour in mathematics. He was the first Australian ever to do so.

Can Terry Tao now solve the twin-prime problem? It is considered to be very, very difficult. But, Terry is very, very smart.