Fastest path not always the shortest

By Burkard Polster and Marty Ross

The Age, 12 May 2008

“Help! help!” Startled, you drop your holiday maths reading to look out at the ocean. To your right, you see a swimmer, far from shore, waving frantically – to your left on the beach, an athletic lifeguard springs into action. What is the fastest way for the lifeguard to get to the troubled swimmer? There is no time to lose, and you immediately begin your calculations.

You may recall that Baywatch’s Pamela Anderson always seemed to choose a straight-line approach (drawn in red). She probably remembered her school geometry, that a straight line gives the shortest distance between two points.

But is the shortest path really the fastest? After all, the lifeguard runs much quicker than she swims. So, perhaps it would be better to minimize the distance swum, by running along the beach to the closest point to the swimmer (drawn in green). In real life, this is the approach that most lifeguards choose.

Let’s consider the situation pictured. We’ll assume that our lifeguard runs at a speed of 8 meters per second and swims at a speed of 1.5 meters per second. With the distances indicated, you calculate that it will take her 56 seconds if she runs along the red straight line, and 47.3 seconds if she takes the green route. So, the green route is significantly faster, and very well may be the difference between life and death.

With a deeper analysis, you calculate that the fastest path is somewhere between the extreme paths above. The angles α and β that pin down the bend of this special route are determined by Snell’s Law, the same law that governs the way light bends when it moves from air to water:

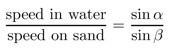
Traveling along this optimal route will have the lifeguard entering the water 8.3 meters earlier, and it will take 46.8 seconds. This gives an extra savings of half a second. Five minutes later, and very happy about your discovery, you look for the lifeguard to tell her how she should proceed.

Of course, by this time the lifeguard has already dragged the swimmer to shore and is busy resuscitating them. But she’ll undoubtedly be pleased to hear that his rule of thumb has the mathematician’s seal of approval.