Melbourne Grammar mystery map

On a recent visit to the Shrine of Remembrance we stumbled across another beautiful shrine, for mathematics. This is the intriguing sculpture at the entrance to Melbourne Grammar School. It is constructed from equilateral triangles and, somehow, is a map of the Earth - Australia and New Zealand are clearly visible in the top right corner. We want to explain what this strange map is all about.

People have been making maps of the Earth for thousands of years and it has always been frustrating, at least since people realised the Earth is Earth-shaped. One would hope that by now we would have devised the perfect map. On such a perfect map countries of equal area would also have equal area on the map, the shortest path between two points would be represented by a straight line, right angles would appear as right angles, and so on.

Alas, there is no perfect map of the Earth, for two quite distinct reasons. First of all there is the "topology" of the Earth: the spherical form of the Earth ensures that certain paths, such as the equator, inevitably loop back on themselves. We cannot faithfully represent all such loops on a map: the only alternative is to rip the Earth apart and to map the tattered remains.

But what if we just wanted to map a small piece of the Earth? Here the second problem, geometry, rears its head. The great 19th century mathematician Karl Friedrich Gauss showed that such a perfect map cannot exist, even for a tiny piece of the Earth.

To see Gauss's argument in action, imagine we want a map of the Arctic. Starting at the North Pole, we could go south a given distance in all directions, marking off a circular region. On a perfect map this region would also appear as a circle, and smaller circles of radius R within the map would have an area of πR². However, this simply must be a distortion of the actual Arctic, since the tried and true formula AREA = πR² is not true for circles around the North Pole. So, if the diameters of the circles are correctly scaled then the areas must be wrong, and vice versa. It is in such measures that the geometry of the Earth is fundamentally different from that of flat maps.

So maps of even small portions of the Earth are doomed to distortion. As a necessary compromise, mapmakers focus on creating specialised maps, serving designated functions extremely well. Examples are aeronautical maps, which preserve important concepts of direction, and the maps commonly found in classrooms, which are generally good compromises and not too distorted in any given way.

Now, back to the topology problem. We still have to decide how to rip the Earth apart, and our mystery sculpture encapsulates one such approach. The idea is to first approximate the spherical Earth by a shape with flat sides. We then cut the shape open along some of its edges and flatten it out, resulting in our map. The shapes that come to mind are the "Famous Five": the regular solids pictured below.

Suppose we choose the cube. Imagining the surface of the Earth just fitting in the cube, a light at the centre of the Earth would then project an image onto the cube. Now cut the cube open and flatten, giving you a map of the Earth. The resulting map is surprisingly similar to more familiar maps.

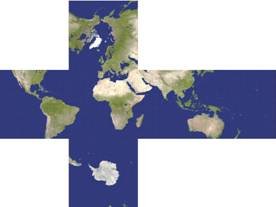
One can do better, by starting with the icosahedron, the last of the regular solids pictured above. With 20 small triangles, the icosahedron hugs a sphere much closer than a cube. Choosing a certain projection, and making the right cuts, you can unfold to give our beautiful sculpture.  (The terrific maps are due to Carlos A. Futuri, who generously allowed us to use them here. You can check out more of his constructions at the link below).

The idea behind such flat projections dates to the 15th century painter Albrecht Dürer. The icosahedron map itself was inspired by Buckminster Fuller, as one of his Dymaxion maps, created in 1954. Actually, the Melbourne Grammar sculpture is missing three triangles from the icosahedron map. We suspect that some less important continent may have been sacrificed for the sake of structural soundness.

Link: http://www.progonos.com/furuti/MapProj/Normal/TOC/cartTOC.html

Copyright 2004-∞ All rights reserved.