One shape to rule them all!

Your Maths Masters are fascinated by balls. In 2010 we pondered a soccer ball, and just a few weeks ago we hit around some tennis balls. This week we want to give the soccer balls another kick.

Take a careful look at the soccer ball above. There’s plenty of pentagons and hexagons, of course, but can you see the cube?

Neither could we. However, we happened to come across a strange variation: 

This second ball is stitched together from 12 pentagons and 20 hexagons, exactly as for a traditional soccer ball. However the colouring is very unusual. The standard pattern consists of black pentagons and white hexagons, but our odd ball is all white except for eight black hexagons.

Eight hexagons, and a cube has eight corners. Yes, it works out: the centres of the black hexagons form the corners of a perfect cube. Very nice!

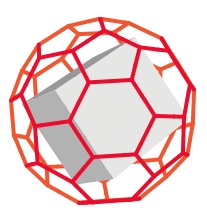
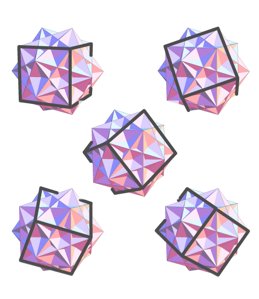
Employing the white hexagons as well, we can find a total of five cubes hiding inside the soccer ball. Together, these cubes form a striking compound shape:

Below we’ve highlighted the separate cubes:

Though we were surprised to stumble upon cubes inside a soccer ball, we probably shouldn’t have been. Almost any highly symmetric solid has at least one cubic companion. To illustrate, let’s investigate the Famous Five: 

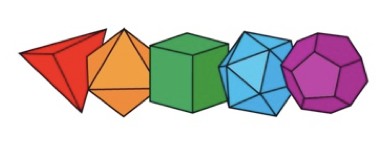
These are the five regular solids: every side is an identical regular polygon and every corner looks like every other. In case some of them are new to you, they’re known as the tetrahedron, the octahedron, the cube (well, duh), the icosahedron and the dodecahedron. 

Since the time of the ancient Greeks, the regular solids have been symbols of symmetry and mathematical beauty. Which is all well and good, but where are the cubes?

To begin, the tetrahedron and icosahedron can easily be found hiding inside a cube:

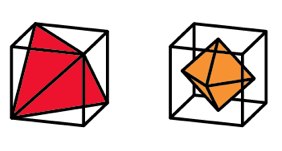
Choosing every second corner of the cube gives the corners of a tetrahedron. And, the centres of the six sides of the cube form the corners of an octahedron. (Alternatively, taking the centres of the eight sides of the octahedron gives the corners of a cube.)

To construct the dodecahedron, we begin as would any good house builder: we take a cube and place a roof over it.

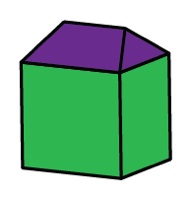
However, we do appreciate strangely mathematical houses. So, we continue and place an identical roof on each of the six sides of the cube. Then, if the dimensions of the roofs are chosen just right, our multi-roofed cube magically transforms into a dodecahedron:

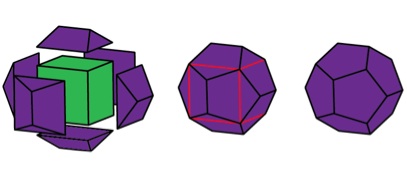
Similarly, we can spot a dodecahedron in our compound of five cubes: 

Returning to our multi-roofed cube, we locate the (red) corners and mark the (orange) points on the squares directly underneath. Together, these 12 points on the cube form the corners of an icosahedron.

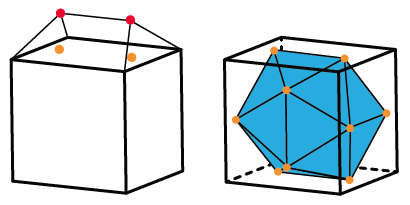
So, there you have it: one shape to rule them all, one shape to find in everything!

Free Public Lecture, Sunday August 11: Burkard will give a presentation titled The dark side of the cube. Come and see Burkard make the cube perform tricks you never imagined possible. He'll be at the Royal Society of Victoria, 8 La Trobe Street, Melbourne, 11:30-12:30. For more information and to register, please visit the MAV website.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators (and iPads) with a hammer.

Copyright 2004-∞ All rights reserved.