Hatcheting a plan

You’re stranded on an island and the not-so-friendly natives are threatening to throw you into the Sacred Tar Pit. Your only hope is to impress them by determining the surface area of the pit. Your only tools: a ruler and your trusty hatchet. Can you do it?

This very contrived scenario could have arisen in an episode of MacGyver. And yes, just as in MacGyver, it turns out that the minimal tools available and some ingenuity will suffice for the job.

Here’s how you do it. Place your (conveniently large) hatchet as pictured below, with the handle just touching at the point M near the middle of the tar pit, and the hatchet blade touching at the point B on the ground outside. 

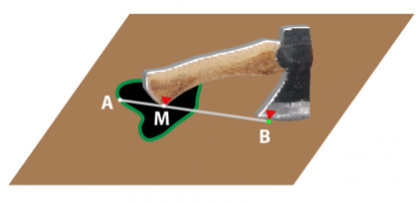
Extend the straight line from B to M until it reaches the far edge of the tar pit, at A. Now drag the handle along the line from M to A, with the hatchet trailing behind. Then drag the handle once around the edge of the pit and back to A; the hatchet should still follow along behind, with the blade always perpendicular to the ground. Finally, drag the handle along the straight line back to M.

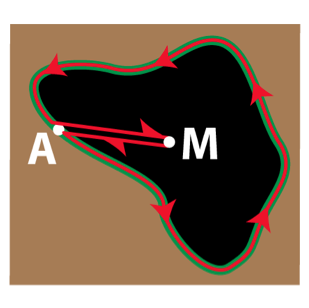
The handle of the hatchet is now back where it began, at M. However, the blade will be at some new point B*.

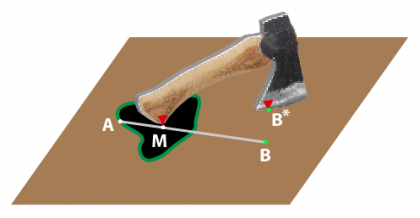
You’re just about done. Measure the effective length of the hatchet (that is, the distance from M to B), and multiply this length by the distance from B to B*. You then proudly declare that this product is the surface area of the tar pit.

What a great trick! The natives are suitably impressed and in gratitude they provide you with a boat to enable you to leave the island. Mathematician MacGyver has triumphed again.

The simple and ingenious measuring device we’ve described is known as a hatchet planimeter or a Prytz planimeter, after its 19th century inventor, Holger Prytz. You can see a planimeter in action here and computer animations here.

Of course there is nothing special about employing a hatchet. Depending upon the size of the region in question, one could use a pocketknife or a bent coat hanger, or even a bicycle (with the front wheel acting as the handle and the real wheel as the blade). Instructions on building your own planimeter can be found here.

Why does the hatchet planimeter work? The first thing to realise is that it doesn’t work, at least not exactly. (Hopefully you’re safely off the island by the time the natives figure this out.)

It is difficult to drag a hatchet handle around the edge of an irregular object with any great precision; attempting this in sticky tar and with threatening natives looking on would be all the harder. However, as well as such practical issues there are also purely theoretical sources of error.

We’ve already hinted at the central problem: the procedure should begin with the hatchet handle at the middle point M of the region being measured, but what is meant by the “middle” of an irregular shape?

For the hatchet planimeter to measure area precisely (in theory), the point M should be at the centre of mass of the region. Unfortunately, unless the region is sufficiently symmetric its centre of mass is just as difficult to determine as its area. In practice, one just tries to choose the point M close to the true centre of mass.

A second source of error is that the distance from B to B* is not exactly the desired length. What is formally required is to consider a circle centred at M with radius the length of the hatchet; this circle passes through both B and B*, and one then measures the length of the circular arc from B to B*. (For other, more sophisticated planimeters, it is not required to determine the centre of mass.)

Subject to the provisos above, the hatchet planimeter can indeed measure the precise area of an irregular region, and in practice can estimate areas quite well. The mathematics to prove this is very pretty but is also very involved. An excellent discussion appears in the wonderful book How round is your circle?, and a brief explanation can also be found here. More of the calculus details can be found here.

Even if the details are involved we can still get a good sense of the proof by considering the motion of the hatchet along special, simple curves. For example, let’s take a hatchet of length 1 and consider the motion of the blade when the handle begins to move at right angles to the hatchet, as pictured below. Indeed we have already met this curve: the blade will trace out a tractrix, which we discussed just a few weeks ago. 

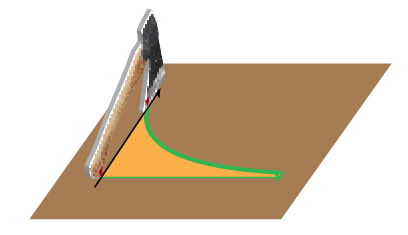
Let’s now figure out the area of the region swept out by the tractrix. That would seemingly be a job for calculus, but there turns out to be a much simpler approach.

In the picture below each blue segment represents the position of the hatchet at a moment in time. 

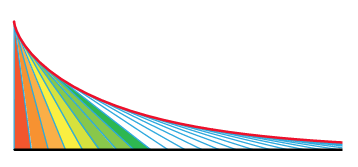
Since each segment has length 1, all of the wedges between the segments are roughly the same as wedges cut from a circle of radius 1. Moreover, when rearranged the wedges fit neatly together, filling the quarter circle as pictured: 

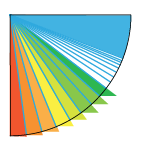
Choosing the wedges smaller and smaller, the wedges will exactly fill up the quarter circle. It follows that the region swept out by the tractrix is exactly the same as the area of the quarter circle, and so equals π/4.

It's a beautiful argument. And, similar arguments for other simple paths can (mostly) justify the workings of the planimeter in general. However, we don't want to give too much away: that might spoil the plot of the next epsiode of Mathematical MacGyver.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.

www.qedcat.com

Copyright 2004-∞ All rights reserved.