A very distant twin

Last week there appeared the kind of mathematical story that we simply love. It was stunning news for mathematicians and just bizarre for most everyone else.

The story, which was first reported in the prestigious journal Nature, concerned prime numbers. That’s not overly surprising: on the rare occasions that mathematics makes the news, primes are often the featured attraction. The great fun of the story is the astonishing appearance of another number: 70,000,000.

Recall that a prime number is a whole number greater than 1 that only has 1 and itself as factors: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 and so on. (Though it doesn’t matter for our story, the reader might ponder why poor little number 1 is excluded from the club.) Individually, prime numbers are very simple, the building blocks of the other, composite numbers.

If each prime is simple, however, collectively they are fantastic and unbelievably frustrating. There is still so much that mathematicians don’t understand about prime numbers.

But let’s begin with some of what mathematicians do know, and perhaps the first question to ask about the collection of prime numbers is of its size: just how many prime numbers are there? The answer is that that there are infinitely many of them.

It is a stunning mathematical truth, and a truth for which calculators and computers are utterly useless. It is one thing to churn out a few, even a few million, prime numbers and to then declare that there always seems to be more primes appearing; it is an entirely different matter to prove that the prime numbers continue forever.

There are many proofs of the infinity of primes and perhaps the earliest known proof, by the ancient Greek mathematician Euclid, is the simplest and the most beautiful. It is a proof that every school student should see, though few will. (The Australian Curriculum is almost silent on prime numbers and doesn’t bother mentioning the infinity of primes until year 12.)

So prime numbers go on forever, but it turns out that they become increasingly rare. About 17% of numbers below 1000 are prime, but only about 8% of numbers below 1,000,000 are prime, and the farther on we look the scarcer they become.

This scarcity is captured by the prime number theorem, proved in 1886 by mathematicians Jacques Hadamard and Charles Jean de la Vallée-Poussin. One way to understand this beautiful theorem is in terms of probability: what are the chances that a randomly chosen number is prime?

Place all the numbers below a billion (10⁹) into a very large hat, close your eyes and then draw out a number. The prime number theorem declares that the chances of your number being prime is about 1/(9 x 2.3), so about 1 chance in 21. Similarly, if we choose a number below a trillion (10¹²) then the chances of that number being prime are about 1/(12 x 2.3), or about 1 chance in 28.

The “about” in those statements sounds wishy washy but it is all made precise by considering probabilities for larger and larger numbers. (In these precise statements the number 2.3 is replaced by log_e(10), the natural logarithm of 10.)

The prime number theorem says a lot, but by no means everything, about the way prime numbers are distributed on average. The Riemann hypothesis, arguably the most important unsolved problem in mathematics, can be phrased as a very careful refinement of the prime number theorem.

As well, though the prime number theorem is a beautiful result about the frequency of primes, it also helps to hide our ignorance. We may know on average how many prime numbers are around but individual primes still tend to appear or not in the most inexplicable manner. For most specific questions about where and how primes appear, the answer is still a mystery.

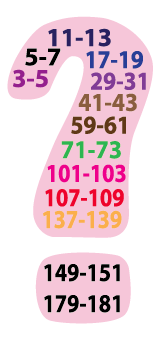
Perhaps the most famous of such mysteries is the twin prime conjecture. Twin primes are pairs of prime numbers that differ by 2, and so are as close as possible to each other. (We'll ignore the number 2, that weird, even prime sitting right next to 3.) For example, 3-5, 5-7 and 11-13 are twin primes. However, the prime 23 is not part of a twin pair since it is sandwiched between the composite odd numbers 21 and 25. The twin prime conjecture then states that there are infinitely many twin primes.

The above examples may suggest that twin primes are common but they become exceedingly rare, and with a little thought it is not difficult to see why. If the chances of a large number being prime is increasingly small, the chances of getting two consecutive primes should be that much harder.

On the other hand, there are infinitely many primes around and the prime number theorem can be used to estimate the chance of a pair of consecutive odd numbers both being prime. Such estimates suggest that, though rare, twin primes “should” keep on occurring; if there is a mathematical god then the twin prime conjecture should be true. But no one knows for certain.

And that, finally, brings us to last week’s news. It had to do with the work of mathematician Yitang Zhang. Did Zhang prove the twin prime conjecture? Well, maybe, almost. In the sense that 70,000,000 is almost 2.

What Zhang reportedly proved was that there are infinitely many prime numbers with a “twin” prime. However, the twin may not just be 2 larger, as 7 is from 5 and 13 is from 11. For Zhang’s theorem, the twin may be up to 70,000,000 larger.

What's an example of a Zhang pair? As it happens 37 and 70,000,037 are both prime, so 37-70,000,037 is a Zhang pair. But the boring old pair 37-41 will do just as well: Zhang doesn't say that the gap will be exactly 70,000,000, just at most 70,000,000.

Yitang Zhang's is an amazing, hilarious theorem. It’s hard to imagine why anyone would care, until you come to appreciate how incredibly difficult it is to prove anything beyond the basics about prime numbers. Before Zhang’s work there was no twin theorem of any type: given an allowable distance of a zillion, no on knew if there were infinitely many prime pairs separated by at most that distance. Yitang’s theorem is simply astonishing.

But is it true? Nature is a highly respected journal but its journalists and editors are not infallible, and here they were merely reporting upon research to appear elsewhere. Zhang's paper has not formally appeared and does not seem to be generally available.

At this stage all is rumor, though the rumors are encouraging. The brilliant mathematician Terry Tao reports that Zhang’s work has been carefully reviewed by experts in the field, and is in the process of being accepted by Annals of Mathematics, the most prestigious journal in mathematics.

And what's your Maths Masters' guess? We guess we'll be silent for once. We know when it's wise to just sit back and wait for the real masters to pass judgment.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.