The magic of the imaginary

One of our favourite mathematical writers is John Stillwell (formerly at Monash University), and perhaps our favourite among John’s many excellent books is Yearning for the Impossible. In this book John describes the manner in which mathematicians fantasize about the “impossible”, and how they make these fantasies real. Bluntly put, John tells the story of mathematics as an extended history of cheating.

Probably the most notorious example of mathematical cheating is the introduction of imaginary numbers. The name hardly instills confidence, and the alternative designation of complex numbers is not much of an improvement.

What are imaginary numbers? The common and unsatisfying answer is that they are, for example, square roots of negative numbers, √–1 and √–2 and so forth.

The eminently reasonable complaint is that a number multiplied by itself cannot be negative, and so these weird roots simply don't make sense. The cheater’s rejoinder is that he doesn’t care whether or not such numbers exist. He’s just going to cheat and pretend that they do.

The cheater’s approach is to avoid asking what imaginary numbers are, or where we might find them, and instead focus upon what they do. That may seem intellectually dishonest but the approach is very common.

Let’s step back and consider an everyday square root, an apparently harmless fellow such as √5. Even here it is very difficult to say what the number actually is. Sure, we can write √5 = 2.36067… blah, blah, blah. However, writing out a few decimals followed by some dots is doing no more than giving the illusion of precision.

To obtain a proper grasp of √5 we need to consider its complete decimal expansion (or, better, consider an entirely different approach). However, it is extraordinarily difficult to make sense of infinite decimals. Indeed, even apparently simple repeating decimals, such as 0.99999…, can be very tricky.

Nonetheless, if we cannot say precisely what √5 is, we still know exactly how it works. The whole point of “root” is that it’s the reverse process of “squaring”. That is,

√5 x √5 = 5

Similarly, we may not believe that √–2 exists, but if we’re going to pretend that it does then the one equation we will definitely accept is

√–2 x √–2 = –2

That’s all good fun but it also appears to be tautological. Is there anything substantial to be gained? Amazingly, there is.

To illustrate, consider the following sequence of numbers:

1, 1, 2, 3, 5, 8, 13, 21, …

These are the megafamous Fibonacci numbers. (They’re not actually due to Fibonacci though, as we'll discuss in a future column, there are other reasons to honor him.) So, we begin with 1 and 1, then 2 = 1 + 1, 3 = 1 + 2, and so on, each Fibonacci number being the sum of the two previous ones. 

That’s all well and good, but what if we want the 1000th Fibonacci number? Sure, we can churn the numbers out one by one: the 9th Fibonacci number is 34, the 10th is 55, and on and on. We’ll eventually get there. But what we want is a formula that will simply provide us with the answer immediately. That’s where the magic begins.

Fibonacci wrote down his famous sequence in 1202. The magic formula, now known as Binet's formula, came over 500 years later. Discovered by French mathematician Abraham de Moivre, Binet's formula gives the 1000th Fibonacci number as

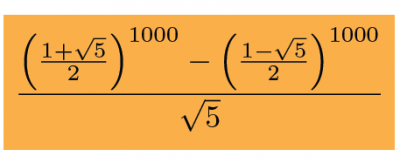
It is hard to exaggerate the amazingness of Binet’s formula. Clearly the Fibonacci numbers will all be whole numbers. Nonetheless, Binet's formula enters the world of irrational numbers and then exits again. All we need use, and all we can use, is that √5 x √5 = 5, and all the irrational roots magically cancel out.

(As an interesting side point, notice the golden ratio (1 + √5)/2 appearing in Binet's formula. It is pleasing to see the golden ratio taking time away from the tawdry business of selling cars to perform an honest day’s mathematical work.)

We can perform exactly the same magic with imaginary numbers. To illustrate, let’s consider another sequence:

1, –1, –5, –7, 1, 23, 43, …

Known for historical reasons as the Marty numbers, they are deservedly much less famous than Fibonacci’s sequence. However, they are constructed in a similar manner.

For the Marty numbers, we begin with 1 and –1. Then, any Marty number is twice the previous number minus three times the one before that. So, the third Marty number is (2 x –1) – (3 x 1) = –5. The 8th Marty number would be (2 x 43) – (3 x 23) = 17, and so on.

And now the question: what if we want the 1000th Marty number? Here it is:

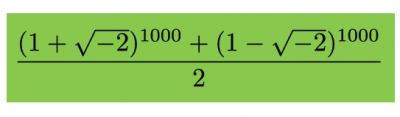
Whereas the Fibonacci numbers required us to consider the irrational, the Marty numbers have led us into the imaginary world. Once again, all the roots magically cancel out, and to accomplish this all we need to apply is the equation √–2 x √–2 = –2.

Not that the Marty numbers are particularly interesting; it is only your Maths Masters and a few of their mates who have ever bothered with them. But the Marty numbers enable a simple and historically faithful demonstration of how to cheat with imaginary numbers.

The practice of employing imaginary numbers to solve problems about everyday numbers has a proud and puzzling history. It began in the 1500s, when Scipione del Ferro and other Italian mathematicians discovered a formula for the solutions to cubic equations (the higher degree counterpart to quadatic equations) Their formula always worked, but sometimes in a perplexing manner: even if the solutions of a polynomial were everyday numbers, the formula might express these solutions in terms of imaginary numbers. Del Ferro and his colleagues had no idea what these imaginary numbers were or why they were necessary. They just knew that they worked.

Cheating with imaginary numbers continued for centuries. The finest mathematicians, including the great Leonhard Euler, becames masters at manipulating imaginary numbers without ever knowing what these numbers were or whether they existed. Euler never properly understood Euler's formula.

Finally, in 1799 the Norwegian mathematician Caspar Wessell explained it all. Wessell provided a convincing explanation of what imaginary numbers actually are, making them as tangible, as "real", as everyday numbers. (They are arguably even more real: it was another 50 years before "harmless" irrationals such as √5 were satisfactorily explained.)

So, did the cheating end? Yes and no. 

By the end of 19th century mathematicians were much clearer on the rules of the game. It was no longer permitted to blithely concoct new numbers without a solid sense of what these new numbers were. Nonetheless, new numbers and whole new mathematical worlds were still being concocted. 

Mathematicians continue to just make things up, just as they always have. There is a famous quote by mathematician Leopold Kronecker:

God made the integers; all else is the work of Man.

Indeed, Kronecker doesn't go far enough. Nobel prize winning physicist Percy William Bridgman responded to Kronecker's quotation:

Nature does not count nor do integers occur in nature. Man made them all, integers and all the rest.

Bridgman was correct: all mathematics is cheating. It's all a fiction.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.

www.qedcat.com

Copyright 2004-∞ All rights reserved.