Hermann the hermit

 

Regular readers of this column may suspect that your Maths Masters hate decimals, and base ten and the metric system. It’s not true. We don’t actually hate decimals and the like; we’re just happier when they’re not around.

However, there is one base ten phenomenon we can never resist: we love a good centenary. It’s our guilty pleasure.

Each year, we search for mathematicians who were born or who died a century ago, or two hundred years ago, and so on, back as far as we can see. It’s a fun way to choose to honour some great mathematicians and some of the long forgotten. And, you never know what mathematics this game of lucky dip will bring forth.

This year we have the opportunity to celebrate the thousandth birthday of German mathematician Hermann of Reichenau. No, we had never heard of him either. However, reading up on Hermann gave us some fascinating insight into medieval mathematics.

Hermann of Reichenau wasn’t exactly a hermit, as our title unfairly labels him, but he didn’t get out a lot. Hermann was severely disabled from childhood, with little ability to walk or speak. He was untactfully referred to as Hermann the Lame, and even less tactfully as Hermannus Contractus.

In the 11th century, European mathematics was in very poor shape. The great achievements of the Greek mathematicians had long been forgotten, and the Indian and Arabic advances were only beginning to find their way to Europe. As such, European mathematics of the time consisted of little more than rudimentary astronomy and arithmetic.

The arithmetic was based almost solely on the clumsy and semi-mystical investigation of number patterns by the 6th century Roman mathematician Anicius Boethius; one historian has described Boethius as "a [giant] among Roman scholars, and a [midget] by the side of the Greek masters". This was Hermann's role model, and those were the times.

Hermann created no original mathematics, but he was an industrious writer and he did his small bit to waken European mathematics from its slumber. Hermann was one of the first to write on Arabic mathematics and astronomy, and as such was responsible for the introduction of the astrolabe (a precursor of the sextant) and other astronomical instruments. It seems that Hermann could not read Arabic, most likely learning his mathematics from the writings of Gerbert of Aurillac, the greatest European mathematician of the era (and a Pope!).

There’s not much more to say about Hermann’s mathematics; it wasn’t thrilling. Except, we have Hermann to thank for introducing us to the craziest board game of all time: rithmomachia.

Once rivaling chess in popularity, rithmomachia is unbelievably complicated. Hermann of Reichenau was responsible for the earliest known manual for the game, and it definitely required one.

“Rithmomachia” translates literally as “the battle of numbers”, which is as good a description as any of the game. (The expression “mathematical Calvinball” also comes to mind.) The game is played on an 8 x 16 board, and the players begin with numbered counters, as pictured below.

Some patterns to the numbers are clear (even if their purpose isn't), and the rest are easy to describe, if seemingly arbitrary. The 153 in the white square on the left, for example, comes from adding 81 + 72 in the adjacent triangles.  

The counters move horizontally and vertically, the same as rooks in chess, but they may only move a specific number of spaces; circles, for instance, may normally only move one space. 

Counters can be captured in a similar manner to chess, by meeting. In the following diagram, for example, Black's circle 7 can capture White's square 15.  However, there are other ways that counters can be captured, and that's where the fun, and the arithmetic, begins.

 

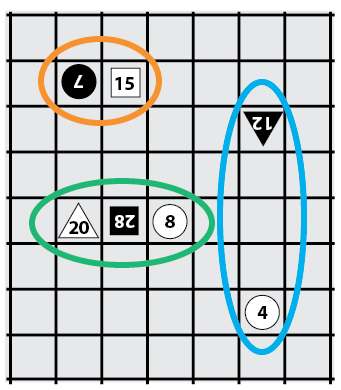
A second way to capture is ambuscade. For example, Black's square 28 above can be captured by ambuscade because it is sandwiched between White's 20 and White's 8, and 28 = 20 + 8. What fun!

But wait, there's more. In the diagram above, White's circle 4 can capture Black's triangle 12 by assault. Why? Because there are 3 vacant squares between the counters, and 4 x 3 = 12! 

Now, take a deep breath. We have to describe how to actually win the game.

There were many ways to win rithmomachia, and the players would agree prior to the game which type of win they were attempting. For example, the goal may be to capture a certain number of counters. Or, the goal may be to have the numbers on the captured counters sum to a designated value. Or, both may be required.

However, those games were for the novices. The true rithmomachia afficionado wanted to play for a Proper Victory. These were obtained by arranging counters in a number sequence. For example, arranging the arithmetic sequence 6, 9, 12, involving both colour counters, would constitute a proper victory.

Then, among proper victories, one was prized most of all: a type of triple win called the Excellent Victory. An example of such a victory is illustrated below. 

 

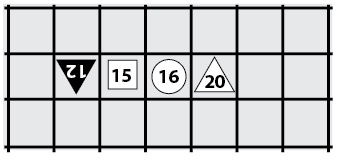
What is so special about these numbers? First, ignoring the 15, the numbers 12, 16, 20 form an arithmetic sequence. Secondly, 20/16 = 15/12 are equal proportions, which was a second type of proper win. Finally, ignoring the 16 and dividing by 60, we obtain 1/5, 1/4, 1/3, which is a harmonic sequence, and a third type of win.

There's plenty more to rithmomachia, all in the same vein. So, anybody keen for a game? Anybody? Hmm. 

It is no surprise that this astonishing game eventually died out, but it's also not surprising that rithmomachia was very popular in Hermann's time. Rithmomachia fitted perfectly with, and offered valuable practice in, the flawed art of medieval arithmetic. 

In the 11th century, arithmetic was wrapped in Boethius's mysticism and it was very difficult. Calculations were still done with Roman numerals and the techniques were clumsy. The memory of myriad special cases played a huge role.

However, once the now-familiar Arabic numerals appeared, and once the power of positional notation was understood, arithmetic lost its mystery, and the era of rithmomachia was set to end. (The gameboard pictured above, featuring Arabic numerals, is from a 16th century English manual, from just around the time interest in the game was waning.)

Indeed, Hermann could have helped end the era. Gerbart of Aurillac included Arabic numerals in his writings, but neither he nor Hermann recognized their true significance. That had to wait for a later, and much greater, mathematician; we'll write of him in the near future.

So, Hermann of Reichenau missed an opportunity to revolutionize European mathematics. But, he did leave us with one crazy board game. That's plenty good reason for us to celebrate him on his thousandth birthday.

 

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.

www.qedcat.com

Copyright 2004-∞ All rights reserved.