Strange moves of a mathematical feast

by Burkard Polster and Marty Ross

The Age, 20 April 2009

The eggs above contain the dates of Easter Sunday from 2006 to 2009. With such an obvious pattern, it is clear that Easter next year will be…who knows!

Well, we do. However the precise rules for determining Easter are strange and intricate. And trying to find a pattern to the Easter dates is anything but easy.

The date of Easter was meant to have been settled by the Catholic Council of Nicaea in 325. In one big mouthful, they declared Easter to be on the first Sunday after the first full moon, on or after the vernal equinox (the moment at which the Sun moves from the northern to the southern hemisphere). This is no longer true.

Why? That’s not so obvious. After all, with the Nicaean concept of Easter it is easy to calculate year by year. For example, this year the equinox was March 20, followed by a full moon on April 9, and then Easter on April 12.

What about next year? Starting at April 9, we mark off time to next year’s equinox, again on March 20. We just count in lunar months, from full moon to full moon, about 29.5 days each. This should get us to a full moon on March 29. Then the following Sunday is April 4, and that’s Easter.

That seems clear and simple to us. Not, apparently, to the Christian scholar Dionysius Exiguus. In 525, Dionysius changed the definition of Easter.

What’s the problem? Well, a minor problem is that lunar months vary in length. This means our calculation above was a bit imprecise. And in fact the full moon next year will occur on March 30, though still leading to Easter on April 4. This is really a non-issue: one can easily be more precise if the timing of the moon warrants it.

It seems that the real issue for Dionysius wasn’t the calculation of Easter for the next year or two. His concern was to calculate all the Easters! Why did he want to do that? God only knows.

Dionysius standardised the dating of Easter, using the Julian calendar of the time. First, he declared the ''equinox'' to be March 21. So, he no longer needed to bother with the actual equinoxes.

Second, Dionysius replaced the calculation of an actual full moon with a theoretical calculation, the Metonic Cycle. Named after the Greek astronomer Meton, this is the observation that 235 lunar cycles takes extremely close to 19 years. Dionysius simply declared 19/235 of a year to be a “lunar month” and used this to count off. Choosing an actual full moon to begin on, Dionysius then happily calculated the dates of hundreds of "moons'', and hundreds of Easters.

Alas, Dionysius used a poor calendar. The Julian calendar included exactly one leap year every fourth year. This was inaccurate, and the Julian calendar fell seriously behind.

The problem was substantially corrected in 1582 by the Gregorian calendar, which is still used today. The key was to eliminate certain leap days, in those years divisible by 100 but not by 400. So, with the length of a year settled, can we now continue with Dionysius’s method?

But wait, there’s more! Pope Gregory did not simply adjust leap years. His scholars also knew that the Metonic Cycle was not exact, and so this was adjusted in a very similar manner. In effect the dates of the full moons were shifted 8 days every 2500 years. With that final adjustment, we have the currently sanctioned method for calculating Easter.

All of the above is precisely mathematical, and so it can all be written out as one big set of equations. The great mathematician Karl Friedrich Gauss was probably the first to explicitly do so. Compiled into one monster equation, here it is:

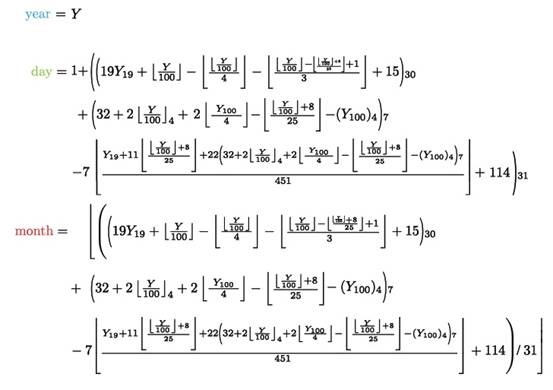
In fact Gauss was not the first to indulge in such calculations. The Jesuit mathematician Christopher Clavius was instrumental in having Pope Gregory accept the new calendar. Ever the optimist, Clavius computed Easter dates up to 80 million years into the future. Should we have told him that by that time the Gregorian calendar will be more than 20,000 days out of sync? Or that by then a year will be only 360 days long? Nah, we didn’t want to spoil his fun.