Proofs without words

Burkard Polster and Marty Ross

The Age, 18 August 2014

Australian mathematics education is in bad shape: the Australian Curriculum, VCE, NAPLAN, teaching materials, teacher training, Tony Abbott, it's all very depressing. And what's the worst of it? The words.

Well, probably not. But mathematics writing can be astonishingly painful: barely comprehensible and excruciatingly dull. Curricula go on and on, fussing over manufactured minutiae, of little interest or benefit to anyone. (Your Maths Masters never realised the importance of recognising that a straight angle has a vertex and arms, nor that "volume" must be distinguished from "capacity".) And it's rare to find a school textbook that anyone bothers to read, that is employed as more than a collection of worked problems and exercises.

But why? Why should mathematics writing be so poor so much of the time? Part of the problem seems to be that writers are intimidated by the astonishing power of mathematical expression. One formula can capture so much and so precisely, the attitude seems to be that the accompanying words just don't matter. Combined with a fearful approach to mathematical rigour, with the belief that one imprecise colloquialism will undo all the careful calculations, the resultant writing tends to be crabbed, legalistic and boring.

We wish writers and teachers were better acquainted with good mathematics writing. It would be wonderful if every (or any) teaching degree had a subject devoted solely to the columns of the brilliant mathematics populariser Martin Gardner. It might then be appreciated that the goal of mathematics writing, as of any writing, is to communicate ideas; above anything else mathematics writing must be clear and engaging.

Perhaps one day mathematics writing will improve. Still, while holding our breath, let's see if we can find a way to get by without the words.

Let's have a look at Pythagoras's theorem. We usually think of this as the equation a² + b² = c² for the sides of a right-angled triangle. However Pythagoras is really a theorem about areas.

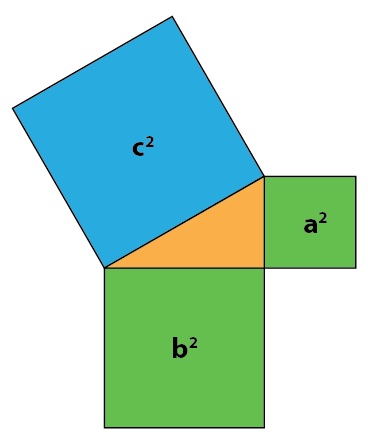
If we place squares on each side of the triangle, as pictured above, then Pythagoras says that the areas of the two smaller green squares sum to the area of the large blue square. Why would that be true?

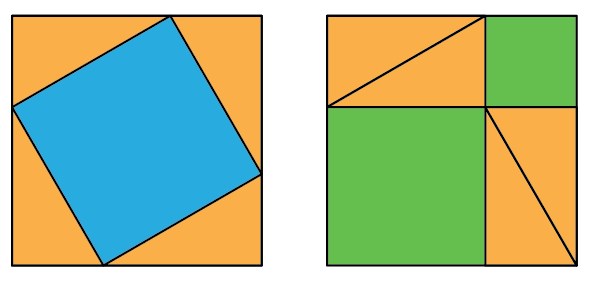
The above diagrams are pretty much all that's required. They show that adding four orange triangles to the blue square results in the same area as adding four orange triangles to the two green squares. Subtracting the orange triangles, we have our theorem.

This is a famous and beautiful example of a proof without words, a proof consisting of a simple diagram or two and little else. Mathematicians love proofs without words, the capturing of a mathematical truth in the most intuitive manner. There are two wonderful books available devoted to such proofs, and one of your Maths Masters has also written a book in a similar spirit.

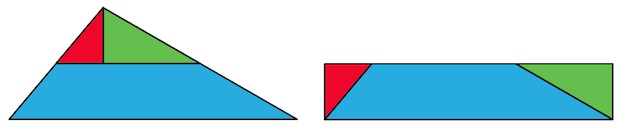
There are many beautiful proofs without words. Similar to our Pythagoras proof, the diagrams below demonstrate the famous "half base times height" formula for the area of a triangle.

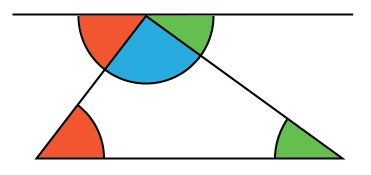
Another beautiful diagram shows that the angles in a triangle sum to 180 degrees:

Geometry lends itself most readily to proofs without words, however many numerical ideas can also be captured with a simple picture. Below we see that the sum of the first few odd numbers amounts to a square. Similarly, the reader should have little trouble calculating the sum 1 + 3 + 5 + ... + 999, simply by imagining the size of the related square.

Proofs without words can be beautiful even when it is unclear what is being proved. Our top picture, of shrinking squares within a square, is intriguing but what if anything does it prove? The reader is invited to ponder.

If this all seems too good to be true, it is. Pictures can too easily be misleading. For example, the above "proof" of the area formula for the triangle won't always work, and the reader may wish to puzzle over what can go wrong. (A similar but more general proof, for the area of a parallelogram, can be found in a previous column.)

It is also clear that the more complicated an idea then the less likely it can easily or faithfully be captured in a simple picture. For example, in last week's column we used diagrams to suggest how any triangle might be viewed as equilateral, however that definitely did not amount to a proof without words. The diagrams were intended to provide some intuition but they also glossed over very tricky details that arise in the proper proof.

There is an inherent uncertainty to proof by pictures, an uncertainty fundamentally at odds with pure and precise mathematics. It is simply too easy to be tricked by a picture and modern mathematics has a deep suspicion of such techniques. Indeed, the incredible revolution in mathematics that began 350 years ago with Newton's calculus can be thought of as eliminating pictures entirely, of turning all mathematics into arithmetic.

But fussy mathematical foundations is one thing and developing intuition is another, especially when the goal is to inspire little maths masters. It is still true that a simple and elegant diagram can capture the heart of a proof and can be convincing in a manner that formulas and words, especially boring words, cannot. And these simple diagrams can also be simply beautiful, a lovely invitation to the rich and wonderful world of mathematics.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is helping Barbie smash calculators and iPads with a hammer.