Geometric proof that √2 is irrational
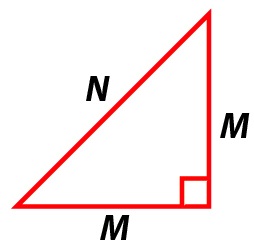
Here is a beautiful geometric proof that √2 is irrational. It has been written up by Tom Apostol (American Mathematical Monthly 107 (2000), pp841-842), but seems to have been known at least a century earlier.We want to prove that √2 is irrational, i.e. that we cannot write √2 = N/M with M and N whole numbers. Squaring and then multiplying by M2, this is exactly saying that we cannot solve the equation 2M2 = N2.

Now think of this geometrically. Pythagoras' Theorem tells us that an isosceles right-angled triangle with hypotenuse N and shorter sides M will result in 2M2 = N2. So, we are trying to prove that there is no such triangle with M and N whole numbers. What we'll do is show that IF there were any such triangle THEN we could always construct a new, smaller triangle, still isosceles and right-angled, and still with whole number sides.
Repeating the construction, we could then make a still smaller triangle, and then a smaller one, and so on forever, always with whole number sides. But that infinite chain of triangles is impossible: no matter where it starts, a decreasing sequence of positive whole numbers cannot go below 1, and so eventually has to stop. And, since the chain of triangles is impossible, the chain could never have started: we can conclude that there could never have been the first triangle to begin with.
So, supposing we have an isosceles right-angled triangle with whole number sides, we have to show how to construct the smaller triangle. To do this, consider the following diagram. The circular arc shows how to position the new edge so that the small triangle is right-angled. And, since a second angle is 45o, the third angle must be as well, and so the small triangle is isosceles.
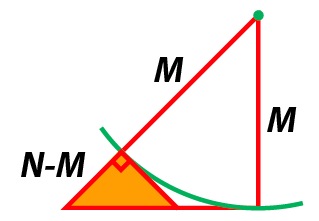
We just have to show that this small triangle has whole number sides. The circular arc shows that the smaller side has length N − M. To figure out the length of the hypothenuse, we just have to note that the three segments highlighted in the diagram below all have this same length N − M.
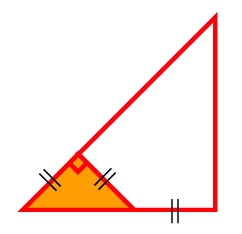
So, the small triangle must have hypotenuse length M − (N−M), which equals 2M−N, definitely a whole number.
![]()
John Conway and Richard Guy presented an origami version of the above proof in The Book of Numbers (Springer, 1995, p183).
There is also a purely numerical version of the above proof, which appeared in A Course of Modern Analysis by E. T. Whittaker and G. N. Watson (Cambridge, 4th ed. 1927, p5). The geometric proof above amounts to showing that if √2 = N/M then also √2 = (2M − N)/(N − M), which would be a fractional representation of √2 with smaller numerator and denominator. Repeating this fraction construction then results in an infinite sequence of fractions, impossible just as the sequence of triangles above was impossible.
To show this new fractional representation directly, we can calculate
√2 = √2 (√2 − 1)/(√2 − 1) = (2 − √2)/(√2 − 1) = (2 − N/M)/(N/M − 1)
Multiplying top and bottom by M, we obtain the promised new expression for √2.
Here is a PDF containing two proofs that √2 is irrational: the proof above and a second, numerical proof. You can also find many more proofs here.