Theatre of the Surd
by Burkard Polster and Marty Ross
The Age, 24 May 2010
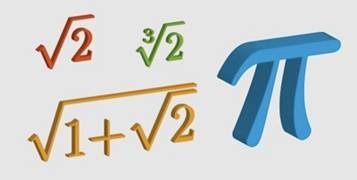
A few weeks ago we wrote about the difficulty of understanding irrational numbers, of going beyond a tautological declaration of "not fractions". One question that arose was the meaning of "surd". This word appears in the draft National Curriculum, and is even the title of a year 10 topic, but it is never actually stated what surds are.
Of course, if everybody already knows what surds are, then all is fine. No such luck. All agree that surds are irrational numbers, but there is broad disagreement on exactly which irrational numbers are surds. In fact, most school textbooks include no clear definition, and the guide to the Victorian Curriculum provides a vague and unhelpful pretend-definition.
All texts make clear that √2 is an example of a surd, but then the focus quickly switches to the "algebra of surds", essentially the consequences of the equation √a x √a =a. A few texts also indicate that π is not a surd, although usually with no explanation. And, the texts agree on little else. For example, whether 1+√2 and √(1+√2) are surds, or whether cube roots and higher roots are included, depends very much upon whom you ask.
In summary, "surd" currently means nothing more precise than "rooty thing". Such vagueness is hardly a sound basis for understanding mathematics, and indeed modern mathematicians seldom if ever use the word. So, what are the origins of "surd", and how did the word lose its meaning?
One of the first to use the word was Leonardo Fibonacci, the famous 13th Century Italian mathematician. "Surd" is derived from the Latin surdus, meaning inaudible or indistinct. This manner of referring to irrational numbers originated with the great Arabic mathematicians of the Middle Ages, whom Fibonacci studied.
The Arabic terminology is unclear (at least to us), and may refer to quite general irrational numbers. However, it seems that Fibonacci's use of "surd" was very specific. For Fibonacci, a surd was the irrational square root of a positive whole number: exactly creatures like √2.
That's a clear and simple meaning, and this meaning may have briefly carried over into English. The earliest reference in the Oxford English Dictionary is to 1551, in which year the Welsh mathematician Robert Recorde wrote of "Quantities, partly rationall and partly surde". Recorde is not at all explicit, but he is presumably referring to numbers such as 1+√2 with √2 being the surd part.
However, this narrow meaning didn't last for long. By 1557, Recorde was willing to include numbers such as 1+√2 and √(1+√2) in the collection of "Compounde Surdes", and he also permitted cube roots. It is fair to say that from this date, and so pretty much always, "surd" had no commonly accepted English meaning.
The Oxford Dictionary actually defines surd as a synonym for irrational number (albeit with some emphasis upon the Fibonacci interpretation). We doubt that the meaning of "surd" ever stretched that far, but it is far from clear.
The trouble is, once the compounding of roots is permitted, it is very difficult to define or to conceive of the huge world of numbers so created. Fifteenth Century mathematicians had little clear sense of irrational numbers beyond the "not fractions" mantra. They did not know whether all irrational numbers could somehow be constructed from roots, and were possibly unable to even conceive of the question.
Consequently, it is usually very difficult to know what early mathematicians meant when they used the word "surd". Most likely, they seldom meant anything precise at all. So, perhaps it is reassuring to witness our schools and our curricula carrying on this proud tradition. Or, perhaps it isn't.
Confusing terminology aside, the underlying mathematical issues were eventually resolved, but it took until the 19th Century to do so. It turns out that there are two precise and distinct concepts of rooty things, and for neither are the earlier surd notions of much help. As for π, it was proved irrational in 1761, and it was only in 1882 that π was proved to not be in any natural sense a rooty thing. It is all a fascinating story, and we hope to write much more of the, um, roots of the story in a future column.
Puzzle to Ponder: Feel free to suggest solutions and ideas in the comments section. Please also email us if you wish to be added to our email list.
Is the following number a surd?
And, for super duper megabonus points, what about this number?
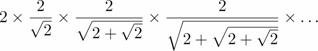
Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.
Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.
Copyright 2004-∞ ![]() All rights reserved.
All rights reserved.