Each year Mathematical Methods is inflicted upon thousands on Victorian Year 12 (VCE) students. Some general indication of the subject's failings can be found here.
Late in 2014 we ran a spot-the-error competition on the 2014 Methods Exams. (Direct links: Thing 1 and Thing 2). Specifically, our competition was to identify "the" multiple choice question in Exam 2 with no correct answer. We had a particular question (Question 4) in mind but unsurprisingly people found plenty to ponder, including some understandable jumping at shadows. What was (perhaps) surprising was that for a long time no one identified the specific - for us, glaring - issue on the specific question that we had in mind. Initially the exams were only available in hard copy, effectively only to Victorian teachers. Once we provided a link to the exams, the question and issue were immediately identified, by two mathematicians (one of whom summed up the exams as "crazy".)
Below we carefully go through Exam 2, commenting on any question that has given us pause, or nausea. There is also much to criticise in Exam 1 - see, for example Question 2, and the proposed solution in the Examination Report. However, in the main Exam 1 is just boring, and boringly easy, rather than silly or wrong.
Section 1 (Multiple Choice)
Question 1: The point P(4,–3) lies on the graph of a function f. The graph of f is translated four units vertically up and then reflected in the y-axis. The coordinates of the final image of P are ...
This is a peculiar question since the function f is effectively irrelevant. Or, as one of our correspondents remarked, one could argue that the final coordinates of P are unchanged: it is only the graph of f that has moved. That may seem somewhat pedantic but it reflects (ha ha) a fundamental confusion in Methods' presentation of transformations: is the x-y world being transformed to a new world, or is it just objects (points, graphs, etc) within that fixed world that are being transformed?
Question 3: The area of the region enclosed by the graph of y = x(x + 2)(x − 4) and the x-axis is ...
This question was a good test of whether the teacher had correctly programmed their student's CAS calculator. For 40% of students the answer is apparently "no". (Yes, the question can be done, more slowly, by hand, a possibility that only makes the question worse.)
Question 4: Let f be a function with domain R such that f′(5)=0 and f′(x) <0 when x ≠ 5. At x = 5, the graph of f has a: A. local minimum; B. local maximum; C. gradient of 5; D. gradient of –5; E. stationary point of inflection.
This was the question that inspired our competition. The intended answer was E, and clearly A-D are all false. However E may also fail to hold for the function f, at least if "inflection point" means the same as in the rest of the world: a change in concavity. As such, an inflection point is fundamentally a second derivative notion and simply will not be implied by hypotheses on the first derivative. (A number of correspondents raised the related but less fundamental issue of whether f having an inflection point at x = 5 requires f"(5) to be defined.)
True, coming up with a counterexample function is not so easy: we present such a construction below. However, even if a counterexample is not obvious it should be obvious that the exam question just smells mathematically wrong. It is also worth noting that there is no universally accepted definition of inflection point, and indeed on (rare) occasion an inflection point has been defined so that E is effectively true by definition. However, since the VCAA (the Methods Authorities) seem never to have bothered to clarify or justify their use of the term, this would be a very weak defence of the question. (We also checked out two Methods textbooks, one of which defined an inflection point in a manner making E true by definition, but without any motivation or explanation. The second textbook was simply wrong, even on its own terms.)
Question 6: The function f: D → R with rule f(x) = 2x3 − 9x2 −168x will have an inverse function for D = ...
Apart from being a silly "look at the pretty picture" CAS exercise, a couple of correspondents argued (or at least thought we might argue) that no such (connected) domain exists: if the domain D is a small enough interval for f to be 1-1 then f will also fail to have range all of R. (Though lazily unbolded, R refers to the set of real numbers, not the range of f.) The point is that in certain contexts a function f: A → B will be considered to have an inverse if and only if f is both 1-1 and onto B. (The same issue was raised with Question 9 on the Exam.) There is a place for such pedantry but that place is not secondary school, and Methods is innocent of the charge here. Note, however, that our correspondents' suspicion was not unreasonable. For example, consider the functions f(x) = log x and g(x) = x. In Methods, the composition function f(g(x)) is not permitted (which is of course insane).
Question 7: The rule of the function whose graph is shown above is ...
All hail the pretty picture! ("is" needs to be replaced by "could be".)
Question 14: If X is a random variable such that Pr(X>5) = a and Pr(X>8) = b, then Pr(X<5|X<8) is ...
Now this was an interesting one. As many correspondents noted, the question is ill posed: there is no definite answer unless we know that Pr(X=5) = Pr(X=8) = 0, and there is just no reason to assume this. (Some correspondents also noted that the problem is undefined if b = 1, though arguably it's a bit nitpicky to consider this an error.)
So how did the examiners handle this? Well, the Examination Report simply discusses the question as if X were a continuous random variable. Curiouser and curiouser, as Alice might say. Of course this unannounced alteration of "random variable" to "continuous random variable" was undoubtedly an oversight: we're sure that the examiners would never stoop to simply pretending that the original question was unproblematic.
Whether a slip of the pen or sleight of the hand, the Report's alteration contains an ironical twist. A continuous random variable is commonly (though far from universally) defined as one which can take on all values in a certain interval; this definition also appears to be common in Methods literature. However, a continuous random variable so defined may still take on particular values with strictly positive probability. (Consider for example tossing a coin, setting X = 0 if the toss is heads, and otherwise sampling X randomly from a normal distribution.) Consequently, the addition of "continuous" in the Examination Report hasn't resolved anything.
Question 19: Jake and Anita are calculating the area between the graph of y =  √x and the y-axis between y = 0 and y = 4. Jake uses a partitioning, shown in the diagram below, while Anita uses a definite integral to find the exact area ...
As one of our correspondents noted, the wording is pretty lazy for a high stakes exam. The partition (no "ing") is simply the set {0, 1, 2, 3, 4}, and can be "used" in a variety of ways.
Question 20: The graph of a function, h, is shown below. The average value of h is ...
The question is fine. However the Examination Report suggests a laborious computation of areas, while the answer is immediately obvious by symmetry.
Section 2
Question 1: The population of wombats in a particular location varies according to the rule n(t) = 1200 + 400 cos(πt/3) ...
A routine trig question pointlessly cloaked in pseudo-modelling. A waste of good wombats.
Question 2: On 1 January 2010, Tasmania Jones was walking through an ice-covered region of Greenland when he found a large ice cylinder that was made a thousand years ago by the Vikings ... Tasmania found that the Vikings made the cylinder so that [the surface area] S is a minimum ...
Oh, those Viking scamps. When they weren't invading this or pillaging that, they could always be found minimising something or another.
Question 2 (cont): On 1 January 2010, Tasmania believed that due to recent temperature changes in Greenland, the ice of the cylinder had just started melting. ... Assume that the cylindrical shape is retained ...
We don't know where the Methods Gang found ice that melts in such a manner, but we're keeping it well away from our gin and tonic.
Question 3: In a controlled experiment, Juan took some medicine at 8 pm. ... The concentration of medicine in Juan’s blood is modelled by the function c(t) = (5t/2)e-3t/2 ...
Little more than CAS-plugging, but not an awful question. The blood concentration model is somewhat artificial, even for a simplified model.
Question 4: Patricia is a gardener and she owns a garden nursery. She grows and sells basil plants and coriander plants ... The heights of the coriander plants, x centimetres, follow the probability density function h(x), where h(x) = (π/100)sin(πx/50) ...
We suspect that Patricia was mistakenly growing wombats.
Question 4 (cont): In another section of the nursery, a craftsman makes plant pots. The pots are classified as smooth or rough. The craftsman finishes each pot before starting on the next. Over a period of time, it is found that if one plant pot is smooth, the probability that the next one is smooth is 0.7, while if one plant pot is rough, the probability that the next one is rough is p, where 0 < p < 1. The value of p stays fixed for a week at a time, but can vary from week to week. The first pot made each week is always a smooth pot.

Question 5: Let f: R → R, f(x) = (x − 3)(x − 1)(x2+3) and g: R → R, g(x) = x4 − 8x ...
It's hardly earth-shattering, but this question actually reflects and requires some mathematical thought (along with the inevitable CAS silliness.) Someone wasn't following the script.
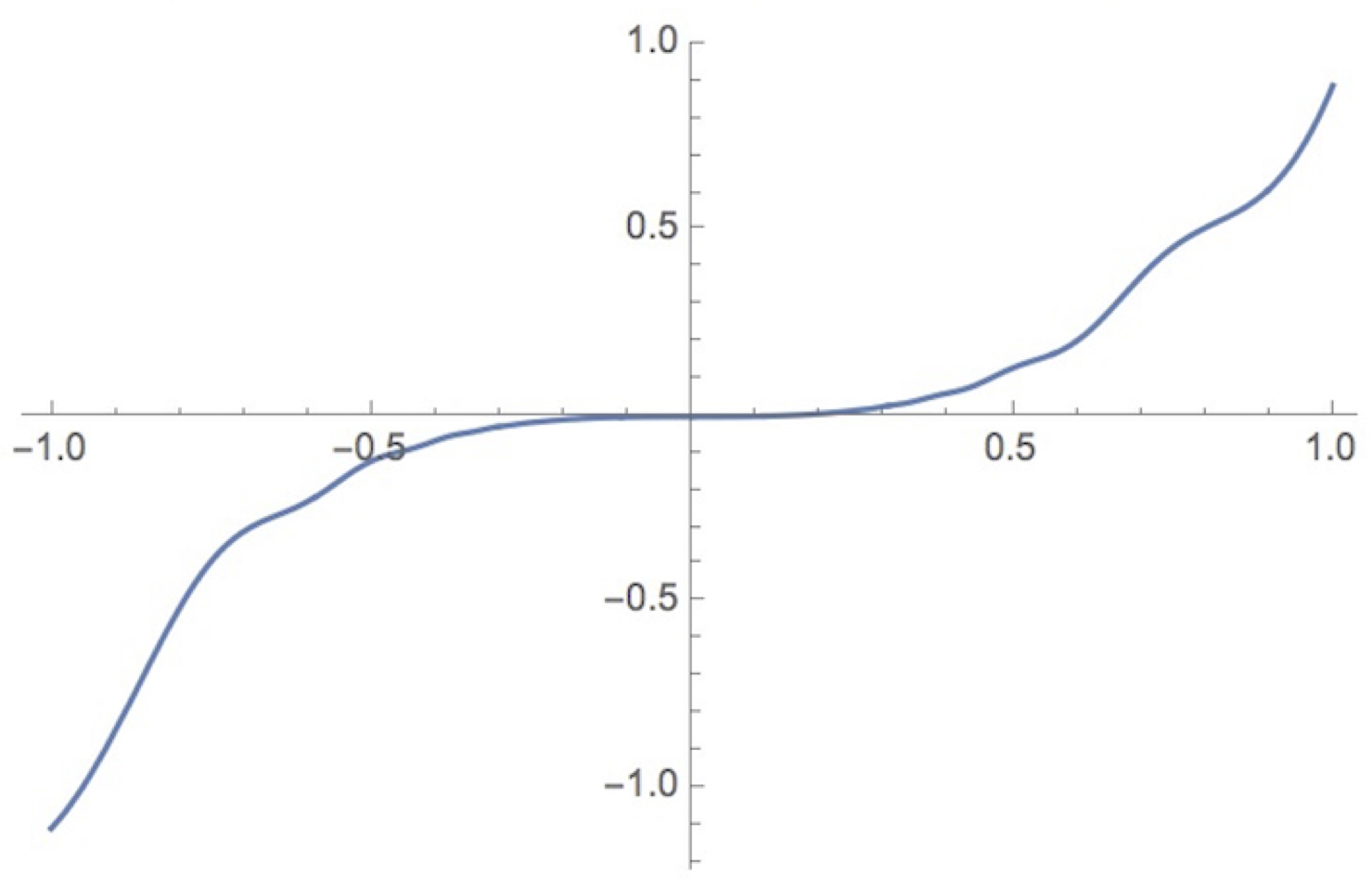
A Counterexample to Question 4
We'll define a twice-differentiable function g on [-1,1] which satisfies g'(0) = 0, g'(x) > 0 otherwise, but with g not having an inflection point at x = 0. It is then easy to transform g (and to extend g to all of R), giving a counterexample to Question 4.
We define g(0) = 0, and otherwise