A very strange set of blocks

The Maths Masters have been lecturing at universities for more than twenty years, and for the last ten years we have been engaged fulltime in popularising mathematics. We have worked long and hard on many projects, but all our efforts have been guided by one fundamental goal: to convince as many people as possible that 0.999... =1.

We look forward to the day when we can visit a school, ask the students what the infinite decimal 0.999... is, and have them all shout back "One!" On that day we can retire happy. It is not likely to be soon.

Infinity is a very tricky concept, which has been bamboozling mathematicians for millennia. In fact it was only in the 19th century that infinite constructions, including 0.999..., were first properly understood.

We have another infinity puzzler in store, so won't revisit 0.999... =1 today (you can read about it here). However, we will pause to note that an infinite decimal is in fact an infinite sum. For example, 0.999... is the infinite sum

9/10 + 9/100 + 9/1000 + ...

A similar and possibly more familiar infinite sum is

1/2 + 1/4 + 1/8 + ...

This sum also totals exactly to 1.

 
A sum where each number is a fixed multiple of the previous number is known as a geometric series. That is true for both the sums above: we’re multiplying by 1/10 to create our old friend 0.999…, and by 1/2 in the second sum.

The nice thing about a geometric series is that, just as for the above examples, the total can be worked out exactly. However, it will come as no surprise that infinite sums other than geometric series can be much trickier.

Consider the following sum, known as the harmonic series:

1 + 1/2 + 1/3 + 1/4 + …

What can we say about it? Well, even though we’re adding progressively smaller numbers, the total is very large. Notice that 1/3 > 1/4, and so

1/2 + (1/3 + 1/4) >1/2 + (1/4 + 1/4) =1/2 + 1/2

 
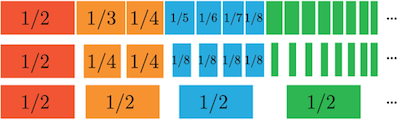
Then, as pictured, the next four (blue) fractions also sum to at least 1/2, as do the next eight (green) fractions, and so on forever. So, since we're adding 1/2 over and over forever, the only possibility is that the harmonic series totals to infinity. We told you it was large!

OK. Now onto another sum, the quadratic series:

1/1 + 1/4 + 1/9 + 1/16 + ...

This time the denominators are squares, and so the sum is smaller. But how small?

Imagine infinitely many squares, the first with side length 1, the second with side length 1/2, then 1/3, and so on. The areas of these squares are 1 x 1, 1/2 x 1/2, 1/3 x 1/3... It follows that the sum of the areas of all the squares is exactly the quadratic series.

 
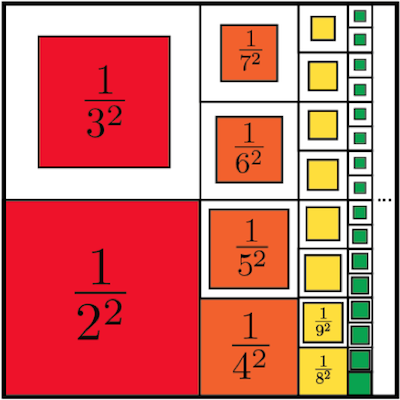
However, as the above picture illustrates, the initial 1 x 1 square is large enough to accommodate all the subsequent squares. That means that the total sum of the areas is at most twice that of the first square. So, the quadratic series totals to less than 2: definitely finite!

We now want to consider a very puzzling toy, suitable for a budding baby maths master. The toy we have in mind is an infinite set of blocks: the first block has dimensions 1x1x1, the second is 1 x 1/2 x 1/2, the third 1 x 1/3 x 1/3, and so on. Let's consider how we could make these blocks.

 
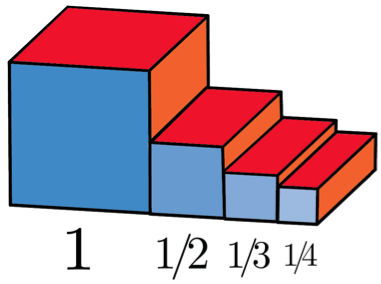
From the familiar "length times width times height", we can calculate the volume of each block. It is then straightforward to calculate that the sum of the volumes of all the blocks is exactly our quadratic series. That means the total volume of the blocks is less than two: it'd take a lot of work to make them, but we'd only require a finite amount of wood.

But what if we wanted to paint the blocks? Just considering the red sides on top, the first has area 1, the second area 1/2, the third 1/3 and so on. That means the sum of the red areas is exactly the harmonic series, and so must infinite!

These are truly strange blocks: it would take a finite amount of wood to make them, but the infinite surface area means it would require an infinite amount of paint to paint them!

But what if we just hollowed out the blocks? It would only require a finite amount of paint to fill them: wouldn't that effectively paint them? It's all very strange!

One final matter: we have yet to say what the quadratic series actually totals to. Believe it or not, we have the precise equation

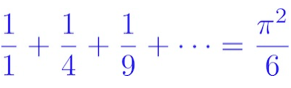
How on Earth did π get in there? In fact, the quadratic series is the starting point for many fascinating stories, on π, and prime numbers, and the famed Riemann Hypothesis.

We'll write more on this soon. In fact, as indicated below, we'll be talking on this as well: everyone is invited! But first, there is some homework to be done: a little matter of 0.999... = 1.

Puzzle to ponder: Can you prove that 1/2 + 1/4 + 1/8 + ... = 1?

Free Public Lecture

Marty will give a talk - Bernhard Riemann's Hypothesis, and What it Means for Mankind - at the Melbourne Museum at 11:30am on Sunday (August 7). For more information and to register, please visit the MAV website.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator. 

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.

www.qedcat.com

Copyright 2004-∞ All rights reserved.