A rectangle, some spheres and lots of triangles

Last week we left you in suspense with an unanswered question: how do we make a mathematically perfect rubber band ball? We answer that below, but we’ll first digress and take a close at the bubble dome, Melbourne’s striking new sports stadium. 

Known officially as the Rectangular Stadium or AAMI Park, the bubble dome consists of pieces of what are approximately geodesic spheres. In turn, a geodesic sphere is a network of small triangles. (Well, in the case of the bubble dome, “small” means having sides about three metres in length). Geodesic spheres became very popular in the 1960s, as an alternative model to conventional rectangular architecture. 

Why would anybody want a spherical house? Well, among all shapes enclosing a given volume, the sphere has the least surface area. So, a spherical house requires less building material and the smaller wall area would result in less heat loss. Geodesic spheres are also light and very stable.

True, there are inefficiencies. It’s not easy to make good use of spherical walls, those edges of the many triangles have to be sealed, and so on. So, though many geodesic homes have been built, there are definite shortcomings.

However, it is very natural to employ a geodesic roof to shelter the rising tiers of a sports stadium. It also looks really cool. Some impressive examples of geodesic constructions are the Montreal Biosphere and the Nagoya Dome.  

A traditional starting point for a geodesic sphere is the icosahedron, one of the famous five Platonic solids. We’ve had occasion to mention these before, when designing silly soccer balls.

An icosahedron has 12 corners, 30 edges and 20 equilateral triangular sides. The corners all lie on a sphere, which the icosahedron roughly approximates. So, the icosahedron can be regarded as a primitive geodesic sphere. To obtain something more refined, we can subdivide each triangle of the icosahedron into smaller equilateral triangles, and then push the new corners outwards until they are also lie on the sphere. The more we subdivide, the better the approximation to the true sphere, as illustrated by the two geodesic spheres below.

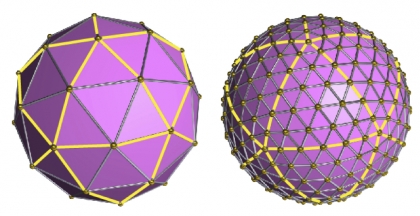
Architectural wizardry aside, your maths masters have recently discovered a beautiful new use for geodesic spheres. They can be used to create ideal, mathematically perfect cousins of messy rubber band balls.

In a standard rubber-band ball, the bands are included as great circles placed any which way. To make the construction less arbitrary, we want a collection of circles that is evenly and symmetrically distributed, and that’s where the geodesic sphere comes in. 

The corners of a geodesic sphere come in diametrically opposite antipodal pairs, just like the North and South Poles on the Earth. Moreover, just as there is the Equator equidistant from the poles, each antipodal pair of corners has an associated great circle. The corners are also very evenly distributed, so if we draw a great circle for each pair of antipodal corners, we should obtain an impressively symmetric model for a rubber band ball. And we do! (Well, there is still the issue how the rubber bands would overlap each other, but we’ll leave those technicalities for the Construction Department.)

Consider the two geodesic spheres we constructed earlier. In what may amount to a world premier, below are the two corresponding rubber band balls. Enjoy!

Puzzle to ponder: How many corners, edges and sides do the above geodesic spheres have? 

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator. 

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.

www.qedcat.com

Copyright 2004-∞ All rights reserved.