The Singapore Triangle

 

Out shopping on a recent visit to Singapore, we stumbled across a huge, beautiful equilateral triangle, composed of smaller black and white triangles. Always on the lookout for energetic maths activities, we asked our junior Maths Masters to count the total number of black and white triangles. In the photo you can see them performing, literally, a running count.

However, more senior Maths Masters prefer less athletic techniques. And there is a very quick method of counting the triangles: just count the number of triangles on one side, and square the number. Here, the Singapore triangle has five smaller triangles on a side, and so there are a total of 5² = 25 triangles.

Is this simple formula a surprise? It shouldn’t be. If you take any figure and scale it by a factor N, then the new figure will have exactly N² times the original area. Our big Singapore triangle can be thought of as a smaller triangle scaled by 5, and so the big triangle has just enough room for 25 small triangles.

Of course, what is neat about equilateral triangles is that the large triangle can be completely tiled with the smaller ones. This is also obviously true for squares, but it cannot be done for the other regular polygons.

We want to demonstrate a couple more lovely features of the Singapore triangle. First, look at the triangle without the checkerboard coloring.

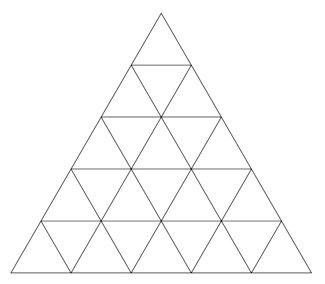
Think of the large triangle as being made up of five rows of small triangles. These rows contain 1, 3, 5, 7, 9 triangles, and so the total number of triangles 1+3+5+7+9.

That is, the sum of the first 5 odd numbers is 5².

Of course, you can see that exactly the same is true no matter what the size of the triangle. So you have a beautiful and simple proof that the sum of the first N odd numbers is N². This means that the next time someone asks you to add up the first thousand odd numbers, you can impress them by immediately announcing that the monster sums to a million.

 

Next, let’s put back the coloring.

Counting only the black triangles in every row we get 1, 2, 3, 4, and 5 triangles. And, counting only the white triangles we get 0, 1, 2, 3, and 4. So, 

(1+2+3+4+5) + (1+2+3+4) = 5²

Adding 5 on both sides of this equation, we find

2(1+2+3+4+5) = 5+5²

Finally, divide by 2, and you have a very nice formula for the sum of the first 5 numbers. And again, the general triangle with N rows gives us a beautiful formula:

1+2+3+ … +N = (N+N²)/2

So, the next time your life depends upon summing up the first thousand whole numbers, you’ll be laughing:

(1000+1000000)/2=500500.

To finish our Singaporean maths games, we pointed out to our junior Maths Masters that each of the smaller triangles consists of four even smaller triangles; we asked them how many of these smallest triangles were used to build the big triangle. Having learned the secrets, it was extremely gratifying to see them forgo another running count, and to instead respond immediately with two correct calculations:

4x25=100 and 10²=100.

 

Puzzle to Ponder: Here some other methods of counting triangles. First, take a look at our last diagram and count the triangles in the vertical columns from left to right: 1 black triangle, two triangles (one black and one white, together forming a diamond), 3 triangles and so on. What general formula does this lead to?

Next, focus on the white triangle in the middle. It is surrounded by 3 black triangles, which are in turn surrounded by 9 white triangles, which are then surrounded by 12 black triangles. What general formula does this lead to?

Melbourne’s Gathering4Gardner – Celebration of Mind, Thursday October 21, 7-9 pm.

 
Burkard and Marty will be hosting this free event celebrating the life of Martin Gardner. It will be held at the MAV headquarters, Cliveden House, 61 Blyth Street, Brunswick. For more information and to register, please go to the MAV website, or call 93802399. Places are strictly limited, so please register early to avoid missing out.

Copyright 2004-∞ All rights reserved.