MathsMaster Chefs

by Burkard Polster and Marty Ross

The Age, 31 May 2010

Cooking shows are all the rage. It seems that every night television chefs compete for culinary honours, and that has given us an idea for another reality show: MathsMaster Chef.

We want to give our show a trial run. So, here are some of our tastiest mathematical dishes, and you can judge how you think they'll fare. Perhaps they could even add some nutrition to current school offerings.

Entrée: Nourishing Nines Nicoise

For this recipe, take the elusive number 0.999..., and prepare the equation M = 0.999.... This will require infinitely many 9s, so try to get them on special. Now, gently multiply both sides of the prepared equation by 10. If you were careful, you should find that 10M = 9.999.... Firmly subtracting the first equation from the second, the result is delectably simple:

Now, quickly divide by 9 and you will discover that M is also equal to 1. So, 0.999... = 1. Very tasty!

Main Course: Traditional Triangle Casserole

To prepare this Greek classic, you will need four red right-angled triangles, and a blue square pot.

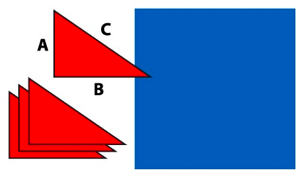
Presentation is everything, so make sure the triangles are identical and are just the right size to fit neatly into the blue pot.

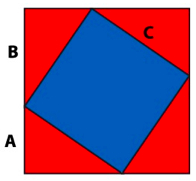
Then the uncovered area of the pot is a square of sidelength C. That gives an enticing blue region of area C². Now, stir the triangles around a bit.

What is our uncovered blue area now? It is C², the same as before. Stir again very carefully...

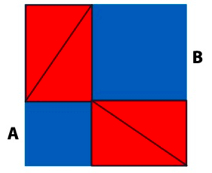
The uncovered blue region still has area C². However, the blue region consists of the two little squares. So, A²+ B²= C². A wonderfully satisfying dish, a gift of that legendary mathematical gourmet, Pythagoras.

Dessert: π-can Pie

Take an appetising circle of radius R, and slice it into an even number of identical wedges. The circumference is a delicious 2πR.

Now, rearrange the wedges into a parallelogram.

Then the area of the circle is 1/2 of its circumference times its radius R. Very sweet! Combine this with the previously prepared circumference, and you can serve up the area of the circle to be πR². What a smart dessert to finish a mathematical meal! (A tip for perfectionist chefs: the more wedges and the thinner they are, the better this recipe will succeed).

So, Judges, what do you think? Will such recipes rocket MathsMaster Chef to the top of the TV ratings?

Puzzle to Ponder: Feel free to suggest solutions in the comments section. Please also email us if you wish to be added to our email list.

Feel free to suggest your own favourite mathematical dishes. And, here is something you can try, using leftovers from preparing the Greek dish above. Take two red triangles and place them in a blue rectangular pot. Stir the triangles until you can see at a glance that the blue parallelogram has the same area as a rectangle with the same base and height.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.