How to beat a chess grandmaster (blindfolded)

by Burkard Polster and Marty Ross

The Age, 10 May 2010

Today is the last scheduled day of the 2010 World Chess Championship, with Veselin Topalov taking on champion Viswanathan Anand. We've watched three weeks of riveting dueling, and now we want to show you how to become a chess grandmaster. Well, at least how to appear so to your friends.

Certain chess greats like to show off by playing multiple games whilst blindfolded. The all-time expert at this was grandmaster George Koltanowski, who in 1960 played 56 simultaneous games blindfolded, winning or drawing them all.

Koltanowski also used to perform an incredible feat. He would ask 64 members of his audience to write a word or phrase of their choice on a piece of paper, and to place them on the squares of a chessboard. Koltanowski would glance at the board and then, blindfolded, he would recite the 64 phrases. Moreover, he would start on a square selected by the audience, and he would recall the phrases by following a knight's tour.

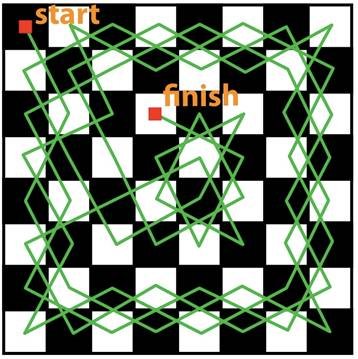
An example of a knight's tour is illustrated above. So, every move is the "two along, one across" move of a knight, and each square is visited exactly once.

Did Koltanowski master this by memorising 64 different tours, one for each starting square? It's possible (for Koltanowski!), but more likely he remembered a single, special tour, one that can be continued as a loop with an extra knight's move.

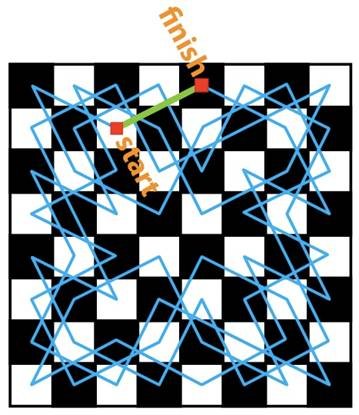
That is still a lot of work, but some loops are much easier to memorise than the tour above, as you can check out here. And, memorising any such loop enables you to perform a Beginner's Koltanowski: you are blindfolded, a member of the audience identifies a square, and then you can recite your tour, just starting on the chosen square.

How about the full Koltanowski trick? There are techniques for rapidly memorising random phrases, but these are not for the faint-hearted. Instead, we suggest a trick that is much easier and is still really impressive.

Our trick requires you to perform a Beginner's Koltanowski, but you must use the blue tour above. Now, suppose you are lucky and the audience have asked you to begin with the square labeled "start". Have them number that square as 64, the next as 63, and so on, counting down to 1.

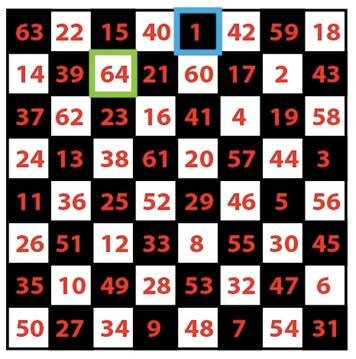
You now choose 16 victims, eight to sum up the numbers in each row, and eight to sum the columns. As you can check, everyone should come out with a sum of 260. That is, what you've constructed is a magic knight's tour: a knight's tour that is also a magic square.

If the audience chooses a different beginning square then the trick will still work, however you must adjust the numbering procedure. The countdown always begins with 64, but for the knight's move from the blue-bordered square to the green-bordered square you must add 63 (instead of counting down 1) to the current number; then, continue counting down as before. It's not difficult to think of a showmanship reason for this jump in the numbering.

That's very impressive, but what if your untrusting friends still doubt your ability to play a game of blindfolded chess? Then you invite the 2010 Championship players to your house, challenging Anand to a game in the dining room, and Topalev in the lounge room.

You let Anand play white, and Topalev will have the black pieces. Once Anand has moved, you stumble, blindfolded, into the lounge room and open with that same move against Topalev. You wait for Topalev's reply, stumble back, and play Topalev's move against Anand. And so on. In the end, you'll have played the two greatest players in the World, blindfolded, and averaged a draw. Who could possibly continue to doubt your ability!

Puzzle to Ponder: Feel free to suggest solutions in the comments section. Please also email us if you wish to be added to our email list.

There is a very simple rule underlying the green knight's tour above. What is it?

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.