The hidden karma of Snakes and Ladders

Burkard Polster and Marty Ross

The Age, 15 September 2014

In a recent column your Maths Masters claimed to enjoy the occasional game of Snakes and Ladders. We lied. Though our little maths masters may delight in the vagaries of pure chance most grown ups, including your Maths Masters, will only play grudgingly, all the while pleading "Dear God, when will this end?"

It turns out that a god is just the right sort of being to answer that question. Snakes and Ladders derives from the old Indian game gyan chaupar, which was imbued with Hindu (or Jain or Muslim) symbolism. The ladders, labelled "knowledge" and "devotion" and so forth, led one to Vaikuntha, the home of the god Vishnu; in opposition, the snakes of "darkness" and "illusion" and the like led the player further away. (In a similar manner many 19th century English versions of the game were cloaked in a Victorian morality.)

Alas, the gods never bothered to tell us how long a game actually takes. But luckily some mathematicians have come to the rescue with a thorough and engaging analysis. To indicate how it works we'll investigate your Maths Masters' version, the game of (singular) Snake and Ladder. In contrast to the familiar 10 x 10 setting, Snake and Ladder is played on a pleasingly small 3 x 3 board and features just one snake and one ladder:

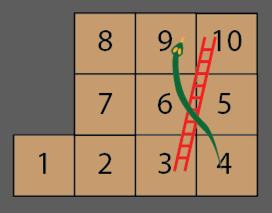
Including the starting 1 square there are ten squares in total, and as usual rolling a die indicates how many squares to move. We'll treat Snake and Ladder as a solo game, which it effectively always is, since one person's progress does not affect any others'.

Let's first ignore the snake and the ladder. Of course each number on the die has a 1/6 chance of being rolled, and then the probabilities of moving from here to there on a given turn are captured by the following 10 x 10 table:

As an example of how to read the table, if we're on the 8th square then the chances of where we'll end up are indicated by the 8th row. Of course with no snakes around there is no chance that we'll wind up on the same square or any earlier square, which is indicated by the zeroes at the beginning of the row. We also have a 1/6 chance of throwing a 1 to take us to square 9, and there's a 1/6 chance of rolling a 2, landing us (finally!) on square 10. There's also a 4/6 = 2/3 chance that we'll throw a 3 or higher, overshooting the final square and meaning we have to stay put. (The finicky S & L gods have decreed that in order to finish the game a player must land exactly on the final square.)

Let's now adjust the table to take account of the snake and the ladder. If we ever land on square 3 the ladder immediately teleports us to square 10 (yay!). So, it is impossible to wind up on square 3 at the end of a turn, and we have a correspondingly increased chance of arriving at square 10. To account for this we add the 3rd column of the table to the 10th column, and then the 3rd column is converted to all zeroes. In the same manner the snake is handled by adding the 9th column to the 4th column and then zeroing the 9th column. These adjustments result in the following 10 x 10 table:

The above table, which we'll call T, is referred to as a transition matrix, and Snake(s) and Ladder(s) is what is known as a Markov process. (It's a genuine Markov process, as opposed to the ill-conceived scenarios one tends to find on VCE exams.) The point is that the above matrix tells us everything we need to know about the probabilities of how the game will progress.

As an example, if we want to know the probability of finishing the game within the first two moves we can calculate T x T = T², the square of the matrix T.

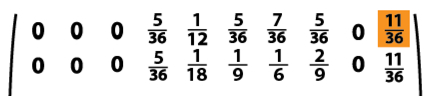
The top part of T² is pictured above, and the final number in the first row indicates that there is a 11/36 chance of finishing the game on the first or second move. Similarly, higher powers of T tell us the chances of finishing the game within three moves, or four moves, and so on. (Since the 3rd and 9th rows and columns of T are redundant, in practice we'd delete them and work with the resulting 8 x 8 matrix.)

But how long on average will a game last? There is no theoretical limit to the length of a game, which suggests that we need to calculate all possible powers of T and somehow sum the results. That sounds tricky and tedious, however sometimes infinite sums have very finite, very simple answers. Such is the case here.

Snakes and Ladders is what is known as an absorbing Markov process: once we arrive at square 9, we simply stay there. That turns out to make the probability calculations very pretty. The (very not obvious) trick is to lop off the last row and column of T, creating a "reduced" 9 x 9 matrix R. Our problem is then to calculate the sum of all the powers of R:

1 + R + R² + R³ + ...

(The beginning 1 of this sum stands for the so-called identity matrix, which in the world of matrices behaves very much like our everyday number 1.)

The above is a "geometric sum" of matrices. We encountered geometric sums of numbers in our last column, as well in many previous columns. There are lovely tricks for calculating these sums and similar tricks can be applied to calculate geometric matrix sums, producing very similar answers.

It's a bit complicated to explain here but having calculated the matrix output of this infinite sum, we can just read off the average length of our game. We simply add the numbers in the top row of the matrix.

It turns out that the average length of a solo game of Snake and Ladder is exactly six moves. That's pretty good, definitely much better than the average of around 40 moves for a 10 x 10 game (depending upon the number and location of the snakes and ladders).

Still, even our 3 x 3 game is too long for a tired Maths Master, just wanting to get the little maths masters into bed. So, we've decided to shorten our game by sneakily including an extra ladder, from 2 to 7.

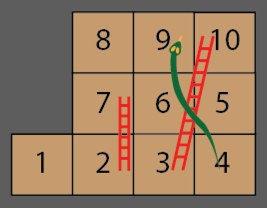
It is easy to adjust the transition matrix to account for our cunning little ladder. Then, summing the matrix powers as before, we find that the average length of our new game is ... exactly six moves.

Huh? How could our new ladder have had no effect?

In fact, the ladder has had two effects. First, as intended, the new ladder gave us a chance of leaping closer to the finish. However a second effect was to create a chance of bypassing the long ladder from square 3 to the finish. As it happened, these two effects exactly cancelled. On larger boards this second effect can easily be much more pronounced, resulting in a significant lengthening of the average game, and thwarting all attempts to hustle the little maths masters off to bed. Similarly, a sneaky snake can actually shorten the average game.

The gods of Snakes and Ladders work in wondrous ways.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is helping Barbie smash calculators and iPads with a hammer.