Squares, triangles and other labour-saving devices

Burkard Polster and Marty Ross

The Age, 17 March 2014

Recently we wrote about logarithms, which are celebrating their 400th anniversary this year. The magic of logarithms is that they can transform an annoying multiplication problem into a much easier addition, at the small price of a couple look-ups in tables. The introduction of logarithms was revolutionary, however it was also a single episode in a very long history. Mathematicians have always been lazy, have always sought to avoid the hard work of multiplying.

How else could we avoid multiplication? Yes, yes, we could use a calculator. However let's concentrate upon historical approaches and leave the discussion of zombie techniques for another day. (Insert Australian Curriculum joke here.)

One remarkable method, which we have mentioned previously, is prosthaphaersis. Discovered in the 16th century this ingenious but clumsy technique applies trigonometric formulas to transform multiplication into addition. Logarithms arrived soon after and prosthaphaersis fell into disuse. But in any case there has to be something easier.

Simplest of all, at least for whole numbers, is to have multiplication tables on hand. For example, if we know our 12 times table then there is no need to calculate 7 x 12: we simply know that the answer is 84. So, it's a good thing we all know our 12 times table, isn't it? (Insert Australian Curriculum joke here.)

It is impractical to memorise multiplication tables of any significant size but we could still hope to have access to written tables. The Babylonians employed multiplication tables over 4000 years ago and such tables have pretty much always been around. (Insert É nah, it's getting too depressing.)

Multiplication tables typically include a very restricted range of multipliers and are intended to aid calculations rather than replace them. But why not simply have a table with a large range of multipliers?

These tables exist. In 1610, the German statesman Herwart von Hohenberg published a 1000 x 1000 multiplication table (reconstructed with an historical introduction by mathematics historian Denis Roegel). In 1820 the German mathematician A. L. Crelle published a table of the same range, which became very popular and is still in print.

The problem is that multiplication tables quickly become prohibitively large. Hohenberg's table(s) was 999 pages long, one page for each multiplier from 2 to 1000; Crelle took some clever shortcuts (as explained by Roegel), making the presentation more elegant, but the end result is of comparable size. However it's done, we have about 1000 x 1000 products, amounting to around a million entries. A table extending up to 10,000 would require around 100 million entries which, at an optimistic 1000 entries per page, would make for a 100,000 page book.

We cannot hope for significantly larger tables but notice that Crelle's tables can also be applied to multipliers that are not explicitly included. For example, his tables can be employed to calculate 38.4 x 2.56 simply by shifting a few decimal points back and forth. As another example, the product 23 x 36,145 can be calculated as the sum of 23 x 145 and 23 x 36,000.

Such arithmetic manipulations can greatly extend the application of multiplication tables and Crelle included instructions for doing so. It also suggests the usefulness of tables of other forms. In 1836 Crelle published product tables up to 10,000,000 for multipliers 2 through 9, and there were many similar tables around at the time. (In 1873 the British Association for the Advancement of Science published a remarkable historical survey of mathematical tables.)

So it turns out multiplication tables such as Crelle's are much more useful than it might first appear. Still, they make for a big book, and there turns out to be a very clever alternative.

Given two numbers A and B a little algebra shows that

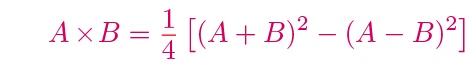
This pretty formula has a striking consequence: if we can calculate squares then it is not much extra work to calculate general products. For example, to calculate 7 x 12 we can set A = 12 and B = 7. Then (12 + 7)² equals 361, (12 - 7)² equals 25, and the difference is 361 - 25 = 336. A quarter of 336 is 84, which is the product we're after.

Though very clever, this method may not seem very helpful: computing squares is hardly more fun than general multiplication. However, if there is a table of squares handy then we'd only have to perform a few additions and subtractions, and a final, annoying division by 4. And the critical point is that tables of squares are much, much smaller than multiplication tables. A table of squares up to 1000, for example, would have just a thousand entries rather than the million-ish for Crelle's multiplication table.

Tables of squares have been around since Babylonian times but it was probably not until the late 17th century that they were used for multiplication. (It is commonly claimed that the Babylonians did so but these claims seem speculative, at best.) In 1690 the Dutch mathematician Johann-Hiob Ludolf published a table of squares up to 100,000 and specifically noted the application of his table to multiplication.

One drawback with the squares method is the annoying division by 4. However if we rewrite our equation as

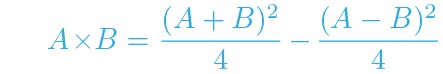
then it is clear what we actually need is a table of Òquarter-squaresÓ, which would circumvent the final division. In 1817 a table of quarter-squares up to 10,000 was created for this very purpose, and in 1887 a table up to 200,000 appeared.

However, there is a second, subtle drawback with the squares (or quarter-squares) method: the method can only be applied if our squares table extends as far as the sum A + B. That's the reason the 1887 table extended to 200,000, so that the product of any two five-digit numbers could be calculated. Slightly more complicated versions of the square formula avoid this problem, but at a significant cost to convenience. However, there is another clever device to avoid this problem: triangular numbers.

Triangular numbers can be obtained by counting the number of dots placed regularly in an equilateral triangle. As pictured below, the sequence of triangular numbers is then 1, 3, 6, 10, and so on.

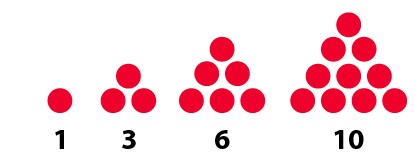
Writing T(N) for the Nth triangular number, it is not all that difficult to show that T(N) is equal to N x (N + 1)/2.

Triangular numbers are natural and interesting, and a large table of them was published in 1762. In 1889, the English mathematician James Glaisher noted that triangular numbers could be used to calculate products, by using the beautiful and simple formula

For example, calculating 7 x 12 once again, we can set A = 12 and B = 7. Then T(11) = 66, T(7) = 28 and T(4) = 10. We then calculate 7 x 12 to be 66 + 28 - 10, which comes to 84. Easy.

For Glaisher's method, the table needn't extend any further than A and B, and it was not much slower than the method of quarter-squares. Nonetheless, the method never caught on. Indeed, quarter-squares never really caught on; though quarter-square tables regularly appeared up until the 1950s, the method never gained the general acceptance that one might expect.

So, what did people actually do, at least what did they do before the triumph of the zombie calculators? It seems that Crelle's table, with perhaps a little arithmetic, were considered quick and easy for many calculations. Otherwise, logarithms were favoured, because of the flexibility of their application.

The quarter-square and triangular methods of multiplication are very clever and very pretty, and it's a shame they were never more appreciated. But sometimes that's the mathematical way of things, that the prettiest is simply not the best.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is helping Barbie smash calculators and iPads with a hammer.