Triangle Surfer Dude

Your Maths Masters are always on the lookout for engaging mathematics and yet again Federation Square suggests something worth pondering. Take a look at the triangular window in the middle of the above photo; it is close to being equilateral and is neatly subdivided by the bars extending at right angles from the edges. There appears to be something there, but what?

To explain we’ll revisit a classic textbook. Harold Jacobs’ Geometry first appeared in 1974 and puts current texts to shame; it is fun, elegantly written and it contains a wealth of beautiful mathematics. Geometry also contains many excellent problems and the very first problem concerns a marooned surfer. 

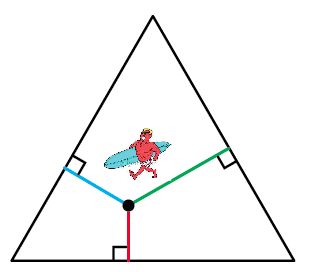
Jacobs imagines a surfer stranded on an island in the shape of an equilateral triangle. (Happens all the time!) Our surfer dude enjoys all of the island’s beaches and plans to spend an equal amount of time at each. That suggests that his hut (if he can be bothered to build it) would be most conveniently located so that the sum of the distances to the three beaches is as small as possible. Where would that be?

The surprising answer is that it doesn’t matter: from any point inside an equilateral triangle the sum of the distances to the three sides is simply the height of the triangle. This lovely result is known as Viviani’s Theorem, named after the 17th Century Italian mathematician Vincezo Viviani. (Viviani is best known as Galileo’s assistant and biographer.)

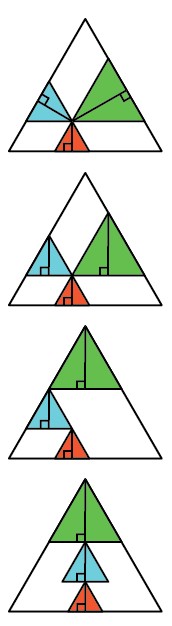
There are many proofs of Viviani’s Theorem but perhaps the most beautiful is a proof without words due to Japanese mathematician Ken-ichiroh Kawasaki. We’ve reproduced Kawasaki’s proof below: just follow the simple mathematical steps from diagram to diagram. 

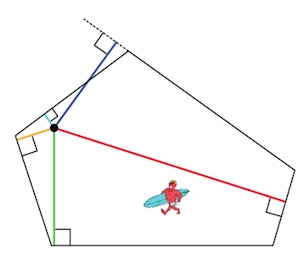
Unfortunately, our Federation square window is not precisely equilateral. It consists of two of Fed Square’s special right-angled triangles, making the top angle about 53 degrees.

What if our surfer’s island was the shape of the window? That’s a more complicated situation but an elaboration of Kawaski’s argument provides the answer: to minimise the sum of the distances the surfer can build his hut anywhere along the base of the triangle. (The answer would be different again if the top angle were greater than 60 degrees.)

Of course the above is all very contrived, since a surfer is unlikely to be marooned on a triangular island. He’s obviously just as likely to be stuck on a quadrilateral or pentagonal or hexagonal island. 

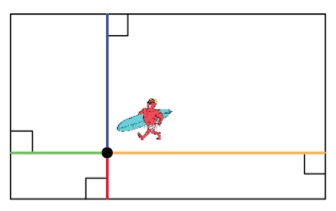
Luckily there are many different islands that possess the build-where-you-like property, and simplest of all are the fabled rectangular islands. On a rectangular island it is completely clear that the surfer can happily build his hut anywhere. What is less clear is that the same is pretty much true for any equiangular polygon.

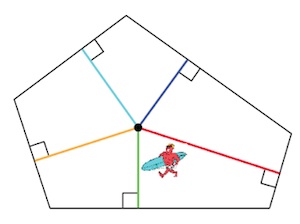
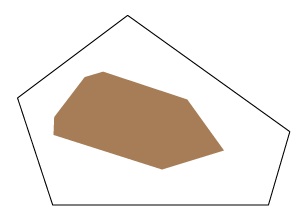
Consider the equiangular pentagon above (with each internal angle 108 degrees). For many points on the island, from which all the beaches can be reached directly at right angles, the sum of the distances will be the same. However, if the surfer builds his hut too close to a beach then one of the natural perpendicular directions may actually take the surfer out into the ocean. 

That is in fact the only thing that can go wrong with an equiangular polygon. A skinny island may have just one best spot on which to build a hut, but a roundish equiangular island will offer a whole region of best spots from which to choose.

So, even a mathematically challenged surfer dude has a pretty good chance of getting it just right on an equiangular island. Life is good in Mathematical Surfer Land.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators (and iPads) with a hammer.

Copyright 2004-∞ All rights reserved.