Super-duper Sudoku

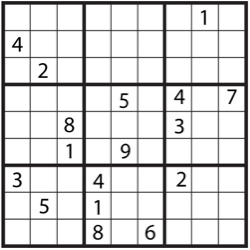
The 6th World Sudoku Championships will be held next week in Eger, Hungary. Australia will be proudly represented by avid sudokuer Sarah Ratcliffe, a professor of biostatistics at the University of Pennsylvania, together with Jill Banks and William Swan. 

We have written previously on Sudoku, and just recently we brushed up on the popular puzzle for our Melbourne museum presentation. And, after a chat with Sarah, we’re in a pretty good position to offer some insight into the world of major league sudoku.

Just in case newspaper puzzle pages are not your thing, here is a reminder of the rules. In a sudoku, numbers chosen from 1 to 9 are placed in a 9 x 9 table, as in the example above. Then, the puzzler must completely fill the table, ensuring that every row, every column and every outlined 3 x 3 mini-square contains each number exactly once.

Sudoku is not really a mathematical puzzle. We could replace the numerals 1 to 9 by any nine distinct symbols and we would have exactly the same puzzle. Nonetheless, plenty of logic is required to solve, and to design, sudokus.

How might you go about building a sudoku? A straightforward approach would be to start with a blank 9 x 9 table and simply go for it: fill in a few squares with numbers so that every row, column and mini-square contains each number at most once. Unfortunately, this may result in an arrangement that cannot be solved. Or, the arrangement may have more than one solution, something that Sudoko designers are also supposed to avoid.

Okay, so let’s try things from the other end, and begin with a completed sudoku. (They’re actually not too hard to do, and you might wish to give it a try). Now, delete a number in some spot, then a next number, and so on. As each number is deleted, we just have to check that the remaining puzzle can be solved in only one way. 

That also seems easy, but again we can quickly run into trouble. Deleting just one number gives a legitimate, albeit ridiculously easy, sudoku. Similarly, deleting two or three numbers will leave a very trivial sudoku with exactly one solution. However, deleting just four numbers can leave an arrangement with two different solutions:

On the other hand, if we choose the spaces carefully, we can safely remove many more numbers. Suppose we take a completed sudoku and then blank out the 21 spaces marked in red in the diagram below. Then, no matter the original completed sudoku, the resulting puzzle can only be solved in that one way.

Of course, all such resulting puzzles are super easy; a super hard puzzle will have to begin with significantly fewer occupied spaces. What’s the minimum number of occupied spaces with which we can begin and still have exactly one solution? No one knows.

Mathematicians have performed extensive searches and have found uniquely solvable sudokus with a mere 17 occupied spaces; the puzzle at the beginning of the column is such an example.  However, no one knows whether there is a sudoku with only 16 spaces filled in.

As a general rule, fewer occupied spaces mean a more difficult puzzle. However, much more important is how the numbers in those spaces relate to each other. For example, the puzzle below has 24 spaces filled by the red numbers, but it is much harder than the puzzle above.

The difficulty of this puzzle is hinted at by the small black numbers. To explain, we’ll focus on the space bordered in green, and we’ll consider what might have to go there. We can immediately rule out the numbers occurring in the row, column and mini-square containing the green space: that leaves just 3 and 4 as possible entries, as indicated by the black numbers.

We can see that there are similar choices for every space in this sudoku. Now, experienced sudokuers have a whole arsenal of logic tricks to apply in such situations. However, for this particular puzzle, none of the tricks help, for any of the spaces!

What this means is that we’re stuck: we simply have to make a guess and to see where this guess leads. That might be to a solved sudoku, or to another dead end, requiring another guess. Possibly good fun on a slow train commute, but nerve-racking in an international competition.

If you’re interested in learning some techniques to solve superhard sudoku, www.sudokuwiki.org is a great place to start. Then, you can give some of the World Championship puzzles a go. With enough practice, perhaps you’ll be joining Sarah, Jill and William in Croatia next year, at the 7th World Sudoko Championships.

Puzzle to Ponder: Consider the diagram with 21 red squares above. As we suggested, if you use a completed sudoku to fill those 21 squares, then the resulting puzzle can only be solved in one way. Can you show this? Is there a similar diagram with 22 squares that works the same way? (We don’t know the answer to this!)

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator. 

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.

www.qedcat.com

Copyright 2004-∞ All rights reserved.