The statistical problem of greedy pigs

Burkard Polster and Marty Ross

The Age, 4 August 2014

Your Maths Masters love games. We're always ready for a sophisticated game of chess, or Go, or Snakes and Ladders. Yep, your Maths Masters are not too old to enjoy games of pure chance, letting the gods of the dice decide our fate. And, we very much enjoy games that require both luck and skill, which makes us big fans of Greedy Pig.

For those unfamiliar with it, Greedy Pig is a simple children's game, played over five rounds. In a given round a die is rolled repeatedly, with each player's total increasing by each number rolled, unless the "killer number" 2 appears. To avoid being killed a player can choose to stop before any roll, locking in their total for that round; the round ends when all players have locked in or when a killer 2 appears, at which point all the greedy players who haven't locked in their scores lose all their points for that round. The winner is the person with the highest score over the five rounds. (Needless to say, there exist many minor variations of the above rules.)

Greedy Pig is a fun game with easy rules. It's also an excellent introduction to the intuition and ideas of probability, making it very attractive as a classroom exercise. So, how does one go about investigating Greedy Pig in a mathematical manner? How does one become Greedy Pig World Champion?

A detailed lesson plan for Greedy Pig is available from the very popular (but paywalled) maths300 education website, and a shorter plan in the same style can be (freely) found at the NSW Government's Digital Education Revolution website. As maths300 describes it the goal is to try to determine the "best strategy" for Greedy Pig. At which point maths300's lesson has already gone somewhat off the rails.

We're not trying to be nitpicky. (If we were, we'd point out to the maths300 writers that the singular of "dice" is "die".) However questions about probability can be very subtle, which means if we're going to be searching for a "best strategy" we really must know what that strategy is supposed to achieve. What is the actual goal? Unfortunately, maths300 never says.

In fact, there is no general "best strategy" for playing the game of Greedy Pig. Maths can help, but winning Greedy Pig will depend more upon psychology, upon evaluating the strategies of your opponents. For example, if you're playing against a number of greedy players then playing "sensibly" may result in you beating most of them but it is very unlikely to make you the overall winner: chances are, a few lucky opponents will choose just the right rolls on which to be greedy. (Exactly the same difficulty arises in trying to win footy tipping competitions.)

OK, so if the maths300 lesson isn't about searching for a best strategy to win the game of Greedy Pig, what then is the goal? What more straightforward mathematical goal might there be?

The point (which is implicit in maths300's lesson) is to not consider greedy Pig as a game against opponents, but rather as a solo game. The individual player is then looking for a strategy to give a good chance of getting a high score. That is, the player wants to try to make her score on average as high as possible. This is now a precise mathematical goal and we can get to work searching for a best mathematical strategy to achieve that goal.

As a lesson, Greedy Pig is intended to be very open and exploratory. Students are encouraged to come up with their own strategies, games are played and outcomes are compared. Then, hopefully, there is extended discussion of why some strategies may be better than others. Why, for example, is "stop after three rolls" not a great strategy?

All this seems natural and good. The lesson is fun and it may well result in some students gaining some genuine understanding of the way probability works, without resorting to formulas or heavy calculation. If students simply learn that dice don't have memories, that every roll provides the same 1/6 chance of killing everyone and no matter how long since the last 2, that would be great. It would put the students well ahead of the thousands of foolish victims blowing their savings on the pokies. Unfortunately maths300 (and DER) goes seriously off the rails.

Exploration and experimentation is all well and good but so are actual answers. So, what is the actual best strategy for averaging a high score on Greedy Pig? How can we determine that strategy?

After all the games, maths300 concludes its lesson with a computer. They decide to "[use] a computer to find the optimal strategy". The various strategies are programmed into the computer, some simulations are run and the winning strategy is declared. Oh dear.

Let's put maths300's computer aside for a moment and get back to actually thinking about the problem. Suppose you happen to have scored 15 points on a round and you want to decide whether it's a good strategy to continue. Well, there's a 1/6 chance that on the next roll your score will go up by 1, and a 1/6 chance your score will go up by 3, and so on; and, there's a 1/6 chance you'll be hit by the killer 2, meaning your score will go down by 15. That means that on average your total on the next roll will change by

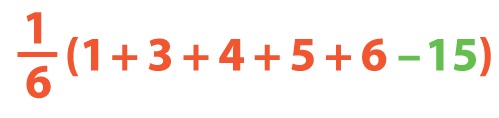
Since the above sum is postive, the conclusion is that if you've only obtained 15 points then (on average) it's worth risking another roll. And what if, more generally, you've already scored a total of T points? Then, on average, the next roll will change your total by

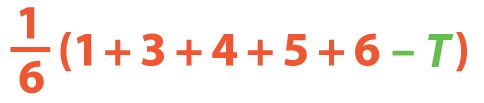
All that matters is whether this sum is positive or negative. The conclusion is that you should keep going until your total on the round is 19 or above, and then stop.

Seriously, how hard was that? How can maths 300 provide fifteen pages of lesson plan without a single mention of this simple and conclusive arithmetic approach?

There seem to be two underlying reasons for maths300's approach, neither all that convincing. The first reason involves the intended audience: the maths300 lesson is supposedly designed for classes from year 3 to year 12, and "attempted explanations involving averaging and long-run frequencies call upon sophisticated concepts that the student may not yet possess".

Fair enough, up to a point. One would of course wish to be gentle with year 3 students, and the formulas above would be too much. However at some level, well below year 12, the simple arithmetic just has to be presented. Indeed, the T formula could be a very natural and gentle introduction to the power of algebra.

Moreover, though the notion of long-term average may be (somewhat) sophisticated, it is also intrinsic to an understanding of the problem, of what the "best strategy" is supposed to achieve. Shying away too much from such ideas makes the whole exercise meaningless.

Bizarrely, maths300 is even reluctant to mention any notion of probability, that the killer 2 has a 1/6 chance of occurring on each roll. Supposedly such an approach "can be mystifying for a student who self-evidently has seen that the 2 sometimes occurs twice in a row and at other times might not occur for 20 rolls". Well, yes, it can be mystifying. It's also exactly the kind of mystification that a classroom lesson on probability and randomness should be confronting head-on.

The second reason underlying maths300's approach is even more concerning: a fundamental hostility to theory and the very notion of proof. The maths300 writers contrast "empirical versus theoretical" methods of learning and teaching and clearly have no respect for the latter. For maths300 it seems that mathematics, whether in year 3 or year 12, is nothing more than an experimental science. The notion that a clear statement of probability or a simple formula for an average may be valuable, may solve the problem in a clean and conclusive manner, seems to carry no weight. (maths300 does offer a "theoretical approach" in an afterthought "Answers" document, however the probability calculations there include none of the simple approach we've outlined above and pretty much answer nothing of interest. It also raises the further question of whether the writers know or care about the difference between a probability and an average.)

Your Maths Masters definitely appreciate the role of computer simulation in teaching Greedy Pig. The repeated rolling of a die can only provide intuition up to a point; after that, to see what "long-term" is really like, one has no choice but to trust the computer and see what happens with zillions of simulated rolls. Moreover, a game needn't be much more complicated than Greedy Pig so that computer simulation is the only way to get a reasonable understanding of the probabilities involved.

However Greedy Pig is a simple game and it does have a simple, and simple to prove, solution. It is absurd to not present this solution to any student, at any level, who has some chance of understanding it.

Your Maths Masters have heard good things about maths300, that many of their lessons are well worthwhile. Maybe, maybe not. However, in the case of Greedy Pig, it appears that a dubious educational ideology has won out over simplicity and mathematical common sense.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is helping Barbie smash calculators and iPads with a hammer.