A Penney for your thoughts

Burkard Polster and Marty Ross

The Age, 28 July 2014

During the school holidays one of your Maths Masters decided to take his junior maths mistress to the zoo. Alas, it was raining cats and dogs. So we changed course and headed for Scienceworks, Melbourne's hands-on science museum. And, it was a zoo.

It turns out than on rainy holidays every one of Melbourne's ten billion children ends up at Scienceworks. Which means that despite the best efforts of the beleaguered staff it takes a drizzly hour just to get inside. Then, once inside, it's chaos, a density of ten million children per exhibit.

Of course even if the parents were frazzled the children were all as happy as could be. They rushed excitedly from exhibit to exhibit, seemingly learning at a hundred kilometres per hour, and at a hundred decibels. Moreover, as a surprise maths masterish treat, it turned out that there was a dedicated mathematics section up and running.

Mathamazing is a travelling exhibition put together by Questacon, Canberra's very impressive science museum. It consists of twenty-two hands-on exhibits, capturing some surprising and beautiful aspects of mathematics. Each exhibit is accompanied by a detailed description, indicating what is being demonstrated.

So, a great thing. Kids having lots of fun and learning some maths in the process. Except, your Maths Masters are not convinced that more than a handful of children learn much of anything.

Sure there are lots of buttons pushed and plenty of things banged. But what do the children learn? What do they understand of what they are pushing and banging, or of the accompanying explanations?

Consider, for example, Penney's game, the subject of one Mathamazing exhibit. The creation of mathematician Walter Penney, the game consists of two players choosing a sequence of three coin tosses, such as TTT or HTT. A coin is then tossed repeatedly and the player whose sequence appears first is the winner. For example, if the sequence of tosses was H H H T H H T H T T then HTT would have won against TTT.

On the face of it Penney's game appears to be pretty boring. If a coin is tossed three times then there are eight possible sequences, each with a 1/8 chance of occurring. So, winning Penney's game would appear to just come down to luck. Surprisingly, that is not the case. For example, it turns out that HTT will beat TTT 7/8 of the time.

In order to understand this let's determine how TTT might win against HTT. Obviously if the tossing sequence begins T T T, which has a 1/8 chance of occurring, then TTT wins immediately. However that turns out be the only way that TTT can beat HTT: after a Heads has appeared, the sequence HTT must occur before TTT.

So, it turns out that in Penney's game some sequences have a better chance against others. Which means it can sometimes be an advantage for a player to choose second, choosing their sequence in response to the first player's choice. What is amazing is that it is always an advantage to go second: no matter the sequence the first player chooses, the second player can always choose a sequence with a better chance of winning.

That seems plain wrong. Surely the first player could simply choose the best sequence and the second player would be stuck with second best. However it turns out that in Penney's game there is no best choice.

The diagram below indicates for each sequence a second sequence that will generally beat it. Some of the indicated probabilities are not too difficult to prove: the reader may like to try showing that HTT has a 3/4 chance of beating TTH. Others are trickier.

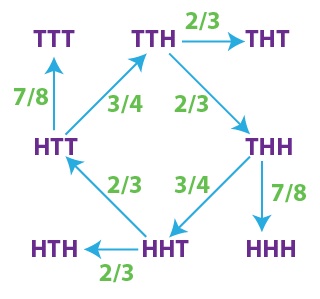
Notice in particular the diamond in the middle of the diagram, representing four sequences in a cycle that better each other. It follows that none of those four sequences can be best overall.

This kind of "no best choice" scenario is referred to as non-transitivity and is actually quite common. It occurs most famously in the game of Rock-Scissors-Paper, where Rock beats Scissors beats Paper beats Rock. Similar Rock-Scissors-Paper competitions can even occur in nature.

Non-transitivity is not in general a surprise, but that it occurs in Penney's game is very counterintuitive. The source of the confusion is considering a long sequence of tosses as a succession of shorter three-toss sequences; those shorter sequences are not independent of each other, and so our intuitive estimate of the probabilities goes awry.

Now what do visitors get out of Mathamazing's version of Penney's game? Not a whole lot.

The Mathamazing version consists of a barrel containing Red and Blue balls. The visitor punches buttons to choose a three-ball sequence and then the computer chooses its sequence; the balls are then drawn at random until either the visitor's or the computer's sequence appears, and the winner is declared. The computer keeps a running tally of its success rate.

It is hard to see what visitors might get out of simply playing this game once or twice. Sure, the majority of the time the computer wins, but often enough the player wins. Whoever wins, it's hard to see why the response should be anything other than "meh". Yes, Mathamazing's Penney exhibit is accompanied by an explanation. Unfortunately, that explanation is long, poorly worded and confusing.

Mathamazing introduces Penney's game with a silly non sequitur question: is it true or false that "In games of chance, if you go first, you're more likely to win"? The reason then provided for the computer's advantage is not exactly wrong, but it's also not quite right. The reasoning implies, for example, that the computer choosing BBB should normally beat RRR, which is false: just by symmetry, the two sequences are equally likely to win.

However it hardly matters what is written to explain the game, since it is clear that almost no one will read it anyway. (How many readers of this column tried to read, let alone understood, the explanation contained in the graphic above?)

Your Maths Master spent a good half hour watching visitors interact with Mathamazing's Penney exhibit. He didn't see a single person, child or adult, do anything other than push the buttons to start the game, watch the machine do its thing, summarise the experience with a "meh" and walk away. Not a single person, child or adult, even attempted to read the provided explanation.

And the same was pretty much true of all the Mathamazing exhibits. Your Maths Master really enjoyed many of the exhibits, and he appreciated their cleverness and mathematical merit; if there had been a concerned and cluey parent or teacher or museum guide on hand to explain what was going on, the exhibits could have been great, fun lessons. But that simply didn't seem to be the case. (We've seen guides perform wonders at Melbourne Museum, and we're not entirely sure why they weren't employed at Scienceworks. However we can make a pretty good guess.)

Your Maths Master never witnessed anybody treating any of the displays as more than peculiar pinball machines. No one appeared to be pondering the mathematical significance of the exhibits, and hardly anyone read a word of the explanations. Which turned out to be wise, since almost all of the descriptions were over-wordy and clumsy to the point of uselessness.

We've picked on Scienceworks in a previous column, and we somewhat regret doing so again. We appreciate what Mathamazing is attempting and kids do probably get something out of the experience. However we're simply not convinced that the kids get all that much, and with proper, informed guidance we believe they could get so much more. Moreover, some of the exhibits and their clumsy explanations really need to be rethought; if an exhibit requires that many words to be explained, words that almost no one will read, perhaps the exhibit simply doesn't work. There do exist stunning mathematical exhibits that require no words at all, and we hope Scienceworks and Questacon are contemplating such exhibits for their future displays.

Your Maths Masters really want to like Mathamazing, and Scienceworks more generally. At the moment, however, we're not convinced that Mathamazing in practice is significantly more educational than a day with the mechanical rides and games at an amusement park. And the amusement park is a lot more fun.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is helping Barbie smash calculators and iPads with a hammer.