Adventures in MathleticsLand
by Burkard Polster and Marty Ross
The Age, 2 September 2013
Once a week it’s Mathletics time for the Maths Master children, and for millions of schoolchildren all around the globe. For the few who are unfamiliar with it, Mathletics is an Australian-based online learning system. It is immensely popular and deservedly so: Mathletics is engaging and is genuinely useful for drills, for the testing and practising of arithmetic and simple geometry, and beyond. But …
Yes, there’s a “but”. It’s the same with almost all maths education materials produced in Australia: honest intentions and good work are sometimes tripped up by confusing and needless mistakes. Mathletics is no exception.
To illustrate we’ll review some of the problematic problems, all from just one (admittedly exceptionally troubling) week of Year 4 Mathletics homework. Let’s begin with an easy one: you simply have to decide which of the shapes below has four lines of symmetry.
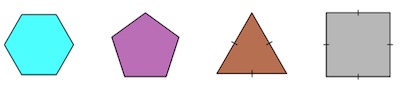
Hmm. The triangle is out, and the square has four lines of symmetry. But what about the hexagon and pentagon? They have a total of six and five lines of symmetry respectively, both then more than satisfying the requirement to have four lines. Nonetheless, as you have probably guessed, Mathletics declares that the square is the one and only correct answer.
Is this nitpicking? Yes and no. Sure, in hindsight it’s not too difficult to figure out that the problem is actually asking for exactly four lines of symmetry. However it is confusingly worded and needlessly so. Moreover, the “equal length” dashes on the triangle and the (presumed) square make matters worse: they only contribute to the problem being less precise and more confusing.
In any case, if it is arguable that our objections to that problem are nitpicky, we doubt that there will be any argument over the next problem. Here, your job is to decide which of the following “shapes” have symmetry:

For some reason Mathletics declares that the chair is not symmetric. Is this simply a mistake? Or, is Mathletics engaging in some weird and misplaced, Magritte-style distinction between the (symmetric) chair and the (asymmetric) picture of the chair? Your Maths Masters have no idea, and we very much doubt that a Year 4 student confronted with the answer would have any idea either.
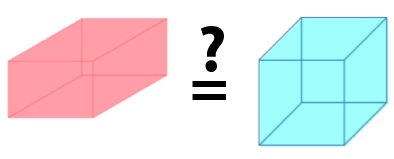
Let’s go on. Your next problem is to locate the “rectangular prism”:
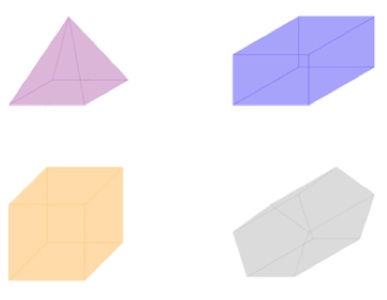
At the outset, your Maths Masters must declare their distaste for prisms. Well, not prisms per se, but we really dislike the word “prism”, and we absolutely detest the expression “rectangular prism”. What on Earth is wrong with “box”? As far as we can tell such jargon, which is never heard outside of a classroom, serves no purpose other than to encourage students to hate maths.
Anyway, back to the problem, and again you probably guessed the intended answer: Mathletics declares the purple figure at the upper right to be correct. But what about the yellow figure at the bottom left? It is presumably intended to represent a cube. But of course, just as a square is a special kind of rectangle, so is a cube a special kind of rectangular prism. It follows that the yellow figure is a perfectly acceptable answer and its exclusion is a blatant and woeful error.
There is also a more subtle issue with the previous problem. At first glance the above pictures may seem to be perfectly fine representations of prisms, but they are not. Real prisms never actually look like that, and it is only years of indoctrination that encourage people to imagine otherwise. What have actually been drawn are parallel projections of prisms, as if the Sun (effectively an infinite distance away) has cast a shadow of wire frames. Parallel projections are easy to draw but they are not very lifelike. And, in an era of excellent and free drawing software there is little excuse for employing them. Isn’t the diagram below much clearer and more elegant?
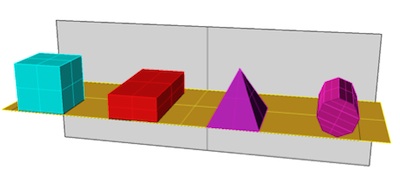
Now, we’ll admit that complaining about Mathletics’ use of parallel projections is definitely straying into nitpicking territory. However, a misunderstanding of such drawings can result in more serious issues. In the next problem you are required to locate the cube:
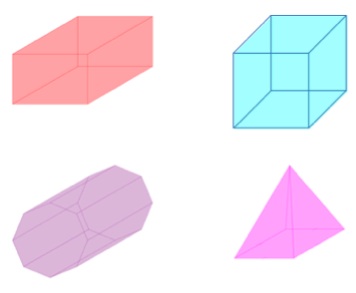
Yes, yes, we all know we’re supposed to click on the blue figure. Nonetheless, the red figure can also arise as the parallel projection of a cube. (That any such “box” picture can result from a parallel projection of a cube is a consequence of what is known as Pohlke’s theorem). As such, there is no sound mathematical reason to prefer the blue figure over the red.
This is still nitpicking? Just wait. Your next problem is to decide whether the figure below represents a square pyramid or rectangular pyramid:
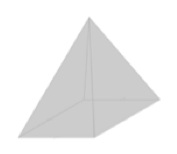
Well, we’ve learned our lesson from the previous problem: the base has exactly the same shape as the base of the red figure above. So, the grey figure must be a rectangular pyramid, right?
Wrong! Mathletics declares it to be a square pyramid. Now that of course means that it’s also a rectangular prism. Except, remember that we're in MathleticsLand, where it seems that squares are not rectangles. Sigh!
By now the message must be clear, but we'll offer one final cherry of a problem to go on top of all this nonsense. Can you determine which of the figures below is a square pyramid?
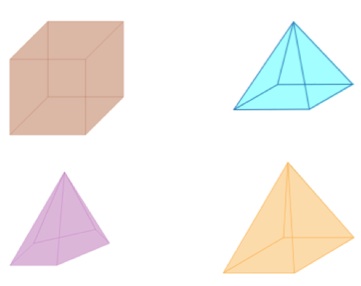
Hmmm. Blue or Yellow? Blue or Yellow? We take a peek back at the previous problem, and we notice that the yellow and grey pyramids are absolutely identical. So, the answer surely must be Yellow.
Wrong again! The "correct" answer is Blue. Why blue? We have no idea. Maybe it’s just that blue things in MathleticsLand tend to be square: it makes as much sense as anything else.
What to make of all this? First, we repeat that we like Mathletics. Despite the clumsiness and the errors it’s a genuinely valuable resource. However, the constant glaring mistakes are just so, so annoying. And, as we remarked earlier, it is by no means just an issue with Mathletics; education materials generally are plagued by such nonsense.
It is also so easily avoided: hire a mathematician. All that is required to dramatically reduce the number of errors, in Mathletics and in any maths ed material, is to employ a concerned, competent and careful mathematician to check the work.
Will it happen? We're not holding our breath.
Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.
Marty Ross is a mathematical nomad. His hobby is smashing calculators (and iPads) with a hammer.
Copyright 2004-∞ ![]() All rights reserved.
All rights reserved.