The Golden Ratio is somewhat tarnished

by Burkard Polster and Marty Ross

The Age, 18 May 2009

Having just written of the beautiful patterns in Angels and Demons, it seems an opportune time to discuss the much less impressive mathematics in Dan Brown’s more famous novel, The Da Vinci Code. Though, to be fair, it’s not all Dan’s fault.

The Golden Ratio, The Golden Mean, The Divine Proportion.... Such grand titles must indicate a truly wondrous concept, yes? Well, yes and no.

The Golden Ratio is perhaps the all-time great mathematical fad. In The Da Vinci Code, the art historian hero Robert Langdon gives an extended lecture on the number 1.618, which he represents as φ, the Greek letter Phi. This number is supposedly the Golden Ratio.

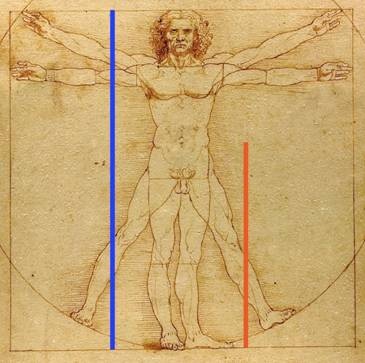
Langdon rattles off an impressive list of the occurrences of φ in art and nature, including the Greek Parthenon and Da Vinci’s Vitruvian Man: both are very familiar to φ-faddists. But, with few exceptions, these supposed occurrences are at best dubious, and at worst plain silly. We can’t cover all of the silliness here (ask us about nautilus shells sometime), but we’ll get started.

The idea of the Golden Ratio dates back more than 2000 years, to Euclid. However the grandiose names and the faddishness began in the 1500s, with the Italian Luca Pacioli.

Needless to say, Euclid and Pacioli did not simply decide that 1.618 was a great idea for a number. In fact, φ = 1.618… (the dots are important, because they indicate that φ is an irrational number) naturally arises as the solution to geometric problems.

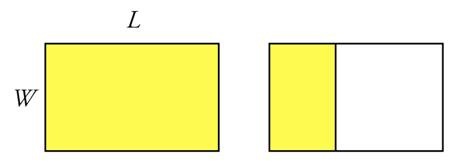
Most simply, we can consider the idea of a Golden Rectangle. This is a rectangle with just the right proportions so that, if we remove a square, what remains is a rotated rectangle with the same proportions. Writing L and W for the rectangle’s length and width, we set φ = L/W to be the ratio of these sides. With a little fiddling, we can then obtain an equation for φ, and the positive solution of this equation is 1.618…

The mathematics of φ is truly beautiful. For example, we can continue to remove squares, creating a descending nest of squares and golden rectangles; this infinite nest has an algebraic counterpart, the beautiful continued fraction

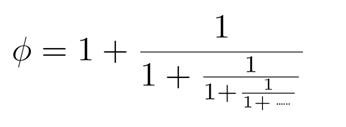
The Golden Ratio is also intimately connected to the famous Fibonacci Numbers – a story for another day.

But what does this mathematical beauty mean for φ’s appearance in art? Very little. Pictures of golden rectangles fitting into the Parthenon are self-evidently contrived. And, there is no evidence that Phidias, the architect of the Parthenon, was aware of the concept of the golden rectangle.

The supposed appearance of φ in the Vitruvian Man is doubly false. The suggestion is that, for a well-proportioned person, their total height divided by the height to their belly button should equal φ. There is simply no evidence that the human body contains φ in any such manner. And, historically the Vitruvian Man is not even modeled upon any theory involving φ.

And it goes on and on. The desire to give art and artists the Golden Ratio seal of approval has led to extraordinary fiddling with numbers and with history. A rose by any other name may be just as sweet, but we wonder how popular φ would be if it were simply known as “Euclid’s Fraction”.